心理学家经过调查发现,某班级的学生对概念的接受能力 与提出概念所用的时间
与提出概念所用的时间 (单位:分)之间满足函数关系:
(单位:分)之间满足函数关系: .其中,
.其中, 值越大,表示接受能力越强.
值越大,表示接受能力越强.
(1)第10分钟时,学生的接受能力是多少?
(2)第几分时,学生的接受能力最强?
(3) 在什么范围内,学生的接受能力逐步增强?
在什么范围内,学生的接受能力逐步增强?
如图,AB=2,BC=5,AB⊥BC与B,l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q。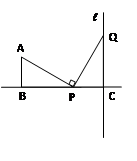
求证:∠A=∠QPC
当点P运动到何处时,PA=PQ?并说明理由。
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
(1)将⊙A向左平移_________个单位长度与y轴首次相切,得到⊙A1.此时点A1的坐标为________,阴影部分的面积S=_________;
(2)求BC的长.
在“5 12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000
12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000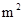 和乙种板材12000
和乙种板材12000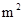 的任务.
的任务.
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30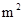 或乙种板材20
或乙种板材20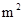 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间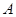 型板房和一间
型板房和一间 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
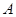 型板房 型板房 |
54 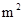 |
26 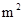 |
5 |
 型板房 型板房 |
78 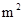 |
41 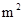 |
8 |
问:这400间板房最多能安置多少灾民?
一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则 ;
;
(2)若∠C为为锐角,则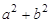 与
与 的关系为:
的关系为:
(3)若∠C为钝角,试推导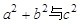 的关系.
的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c;若△ABC是钝角三角形,求第三边c的取值范围.
某文具商店共有单价分别为10元、15元和20元的3种文具盒出售,该商店统计了2011年3月份这三种文具盒的销售情况,并绘制统计图如下: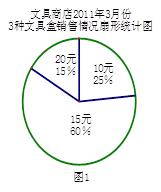

(1)请在图2中把条形统计图补充完整;
(2)小亮认为该商店三月份这三种文具盒总的平均销售价格 (10+15+20)=15元,你认为小亮的计算方法正确吗?如果不正确,请计算总的平均销售价格.
(10+15+20)=15元,你认为小亮的计算方法正确吗?如果不正确,请计算总的平均销售价格.