一位蹦床运动员仅在竖直方向上运动,蹦床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来,如图所示。设运动过程中不计空气阻力,g取10m/s2。结合图象,试求:
(1)运动员的质量m;
(2)运动过程中,运动员的最大加速度;
(3)运动员离开蹦床上升的最大高度。
如图所示,在xOy平面上第一象限内有平行于y轴的有界匀强电场,方向如图。有一电子先后两次以相同的初速度垂直于y轴从P点射入电场中,当匀强电场的场强为E1时,电子从A点射出,A点的坐标为(xA,0),当匀强电场的场强为E2时,电子从B点射出,B点的坐标为(xB,0),求匀强电场的场强E1、E2大小之比;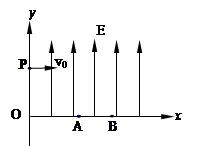
如图所示,质量为m=0.2kg的小物体放在光滑的 圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角
圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角 =37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
=37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
(1)物体第一次滑到圆弧底端A时对圆弧的压力为多少?
(2)物体第一次滑到水平轨道与右侧斜面轨道交接处B时的速度大小
(3)物体第一次滑上右侧斜轨道的最大高度(取g=10m/s2,cos37°=0.8,sin37°=0.6)
如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的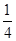 光滑圆弧轨道,轨道上端切线水平,N为待检验的固定曲面,该曲面在竖直面内的截面为半径
光滑圆弧轨道,轨道上端切线水平,N为待检验的固定曲面,该曲面在竖直面内的截面为半径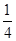 的
的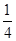 圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点,M的下端相切处置放竖直向上的弹簧枪,可发射速度不同的质量m=0.01Kg的小钢珠,假设某次发射的钢珠沿轨道恰好能经过M的上端点,水平飞出后落到N的某一点上,取
圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点,M的下端相切处置放竖直向上的弹簧枪,可发射速度不同的质量m=0.01Kg的小钢珠,假设某次发射的钢珠沿轨道恰好能经过M的上端点,水平飞出后落到N的某一点上,取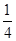 ,求:
,求:
(1)该钢珠经过M上端点的速度大小为多少?
(2)发射该钢珠前,弹簧的弹性势能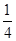 多大?
多大?
(3)钢珠落到圆弧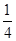 上时的速度大小
上时的速度大小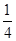 是多少?
是多少?
一束初速度不计的电子在经U的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离d,板长 ,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间。已知电子质量为m,电荷量为e,求:
,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间。已知电子质量为m,电荷量为e,求:
(1)电子离开加速电场是的速度大小;
(2)电子经过偏转电场的时间;
(3)要使电子能从平行板间飞出,两个极板上最多能加多大电压?
(4)电子最远能够打到离荧光屏上中心O点多远处?
如图,水平匀强电场的电场强度为E,一个带电小球质量为m,轻质的绝缘细线长为L,静止时小球位于A点,细线与竖直方向成37°角,重力加速度为g,(sin370=0.6;cos370=0.8)求: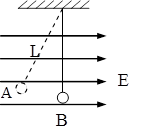
(1)小球带何种电荷?电荷量多少?
(2)现将小球拉回到竖直方向(图中B点),后由静止释放,小球通过A点位置时的速度大小是多少?
(3)若将小球到水平方向(图中C点)由静止释放,则小球通过A点位置时细线对小球的拉力为多大?