(本小题满分14分)
（1）在平面直角坐标系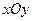
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
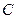．求出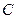的方程及其离心率
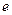的大小；
（2）已知椭圆的一个顶点为A（0，-1），焦点在x轴上.若右焦点到直线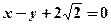
的距离为3.求椭圆的方程
在△ABC中，角A、B、C的对边分别为a、b、c，若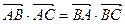
（1）判断△ABC的形状
（2）若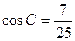
，求
的值
（本小题满分14分）
数列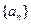
的前n项和为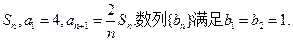
（I）求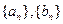
的通项公式；
（II）求证：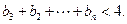
（本小题共12分）
已知函数
的导函数为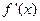
，且不等式
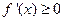的解集
为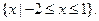
（I）若函数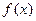
的极大值为0，求实数a的值；
（II）当x满足不等式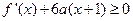
时，关于x的方程
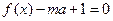有唯一实数解，求实数m的取值范围。
（本小题共12分）
已知双曲线
过点A（2，3），其一条渐近线的方程为
（I）求该双曲线的方程；
（II）若过点A的直线与双曲线右支交于另一点B，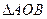
的面积为
，其中O为坐标原点，求直线AB的方程。
（本小题共12分）
在直三棱柱ABC—A1B1C1中，AA1=1，AB=2，AC=1，
，D为BC的中点。
（I）求证：平面ACC1A1⊥平面BCC1B；
（II）求直线DA1与平面BCC1B1所成角的大小；
（III）求二面角A—DC
1—C的大小。