(本小题满分14分)
在平面直角坐标系 中,已知圆
中,已知圆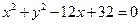 的圆心为
的圆心为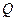 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆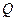 相交于不同的两点
相交于不同的两点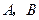 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)是否存在常数 ,使得向量
,使得向量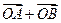 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
|
满意 |
不满意 |
|
|
男顾客 |
40 |
10 |
|
女顾客 |
30 |
20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附: .
|
P( K 2≥ k) |
0.050 |
0.010 |
0.001 |
|
k |
3.841 |
6.635 |
10.828 |
已知
(1)当 时,求不等式 的解集;
(2)若 时, ,求 的取值范围.
在极坐标系中,O为极点,点 在曲线 上,直线l过点 且与 垂直,垂足为P.
(1)当 时,求 及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
已知函数 .证明:
(1) 存在唯一的极值点;
(2) 有且仅有两个实根,且两个实根互为倒数.
已知 是椭圆 的两个焦点,P为C上一点,O为坐标原点.
(1)若 为等边三角形,求C的离心率;
(2)如果存在点P,使得 ,且 的面积等于16,求b的值和a的取值范围.