已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,用1,2,3,4表示命中,用5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为 ( )
| A.0.35 | B.0.30 | C.0.25 | D.0.20 |
已知函数① ,②
,②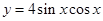 ,则下列结论正确的是()
,则下列结论正确的是()
A.两个函数的图象均关于点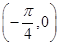 成中心对称 成中心对称 |
B.函数①的图象的纵坐标伸长为原来的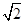 倍,横坐标缩小为原来的 倍,横坐标缩小为原来的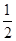 ,再向左平移 ,再向左平移 个单位即得②的图象 个单位即得②的图象 |
C.两个函数在区间 上都是单调递增函数 上都是单调递增函数 |
| D.两个函数的最小正周期相同 |
已知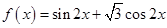 ,在直角坐标系下利用“五点法”作
,在直角坐标系下利用“五点法”作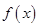 在区间
在区间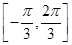 上的图象,应描出的关键点的横坐标依次是()
上的图象,应描出的关键点的横坐标依次是()
A. , ,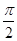 , , , , , , |
B.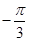 , , , ,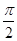 , ,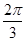 , , |
C.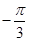 , , , , , ,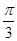 , , , ,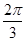 |
D.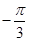 , , , ,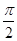 , , , , , ,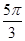 |
已知函数 (
( ),下列说法正确的是()
),下列说法正确的是()
A. 在区间 在区间 ( ( )上单调递增 )上单调递增 |
B. 的图象关于点 的图象关于点 中心对称 中心对称 |
C. 的图象关于直线 的图象关于直线 对称 对称 |
D. 的图象向右平移 的图象向右平移 个单位得到的 个单位得到的 的图象关于点 的图象关于点 中心对称 中心对称 |
函数 (
( ,
, ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 ()
()
A. |
B. |
C. |
D. |
若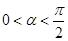 ,
, ,
,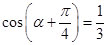 ,
,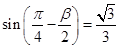 ,则
,则 ()
()
A. |
B. |
C. |
D. |