如图12所示的方格纸中,点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
(1)过点C画OB的垂线,交OA于点D,该垂线是否经过格点?若经过格点,请在图中标出垂线所经过的格点;
(2)过点C画OA的垂线,垂足为E.
① 线段CE的长度是点C到 的距离, 是点D到OB的距离;
② 因为直线外一点与直线上各点连接的所有线段中,垂线段最短, 所以线段CD、CE、OD、OC这四条线段大小关系是 (用“<”号连接);
所以线段CD、CE、OD、OC这四条线段大小关系是 (用“<”号连接);
(3)过D点画直线DF∥OB,若∠AOB=x°,则∠ADC=" " (用含x的代数式表示).
我国出租车收费标准因地而异,A地为:行程不超过3千米收起步价10元,超过3千米后,每增加1千米加价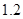 元;B地为:行程不超过3千米收起步价8元,超过3千米后,每增加1千米加价
元;B地为:行程不超过3千米收起步价8元,超过3千米后,每增加1千米加价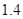 元。(不足1千米的行程,A、B两地均按1千米记费)。小王由A地到B地工作,若用
元。(不足1千米的行程,A、B两地均按1千米记费)。小王由A地到B地工作,若用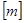 表示大于或等于
表示大于或等于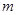 的最小整数(如
的最小整数(如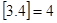 ),请根据下列三种情况分别求出小王在
),请根据下列三种情况分别求出小王在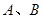 两市乘坐出租车的总花费。
两市乘坐出租车的总花费。
(1)在A市乘坐出租车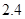 千米,在B市乘坐出租车2.8千米。
千米,在B市乘坐出租车2.8千米。
(2)在A市乘坐出租车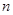 千米,在B市乘坐出租车
千米,在B市乘坐出租车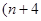 )千米。其中
)千米。其中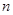 为不超过3的正整数。
为不超过3的正整数。
(3)在A市乘坐出租车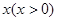 千米,在B市乘坐出租车
千米,在B市乘坐出租车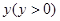 千米。
千米。
某自行车厂为了赶速度,一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产辆与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
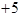 |
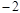 |
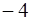 |
 |
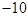 |
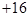 |
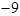 |
(1)根据记录可知第一天生产辆
(2)产量最多的一天比产量最少的一天多生产多少辆?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一辆车的工资为60元,超过计划完成任务每辆车则在原来60元工资上在奖励15元;比计划每少生产一辆则在应得的总工资上扣发15元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
已知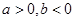 且
且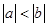 试化简:(1)
试化简:(1)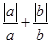 (2)
(2)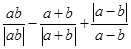
当 时,求下列各代数式的值:
时,求下列各代数式的值:
(1) (2)
(2)
 互为相反数, c与d互为倒数,
互为相反数, c与d互为倒数,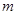 的绝对值是5,试求代数式
的绝对值是5,试求代数式 的值.
的值.