(本小题满分16分)已知常数 ,函数
,函数
(1)求 的单调递增区间;
的单调递增区间;
(2)若 ,求
,求 在区间
在区间 上的最小值
上的最小值 ;
;
(3)是否存在常数 ,使对于任意
,使对于任意 时,
时, 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C(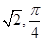 ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈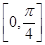 , 直线
, 直线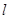 的参数方程为
的参数方程为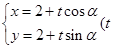 为参数), 直线
为参数), 直线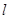 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C, D
两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.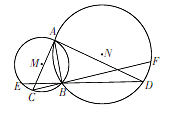
(Ⅰ)求AB的长;
(Ⅱ)求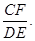
己知函数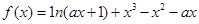 .
.
(Ⅰ)若 x = 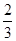 为 f (x)的极值点, 求实数a的值;
为 f (x)的极值点, 求实数a的值;
(Ⅱ)若 y =" f" (x)在[l, +∞)上为增函数, 求实数a的取值范围;
(Ⅲ)若a=-1时, 方程 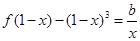 有实根, 求实数b的取值范围.
有实根, 求实数b的取值范围.
已知F1F2是椭圆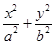 =" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1,
=" 1" (a > b > 0)的两个焦点, O为坐标原点, 点 P(-1,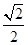 )在椭圆
)在椭圆
上, 且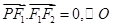 是以F1F2为直径的圆, 直线
是以F1F2为直径的圆, 直线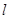 : y=kx+m与⊙O相切, 并且与椭圆交于
: y=kx+m与⊙O相切, 并且与椭圆交于
不同的两点A、 B.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当 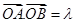 , 且满足
, 且满足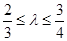 时, 求弦长|AB|的取值范围.
时, 求弦长|AB|的取值范围.
如图所示的茎叶图记录了甲、 乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模
糊, 无法确认, 在图中以x表示.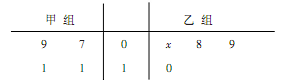
(Ⅰ)如果乙组同学投篮命中次数的平均数为 , 求x及乙组同学投篮命中次数的方差;
, 求x及乙组同学投篮命中次数的方差;
(Ⅱ)在 (Ⅰ)的条件下, 分别从甲、 乙两组投篮命中次数低于10次的同学中,各随机选取
一名, 求这两名同学的投篮命中次数之和为17的概率.