：如图，在平面直角坐标系xoy中，抛物线y＝
x2－
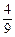x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)
（1）求A，B，C三点的坐标和抛物线的顶点坐标；
（2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程；
（3）当t∈（0，
）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；
（4）当t为何值时，△PQF为等腰三角形？请写出解答过程．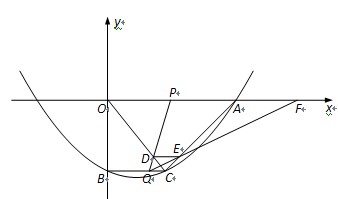
.设函数
且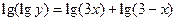
。
（Ⅰ）求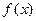
的解析式及定义域。（Ⅱ）求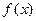的值域。
已知函数
.
（Ⅰ）当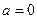
时，求曲线
在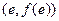
处的切线方程（
）
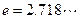（Ⅱ）已知
为函数
的极值点，求函数的单调区间。
（本小题满分10分）选修4-5：不等式选讲
已知函数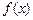
=|x-2|
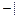x-5|．
（I）证明：
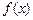≤≤3；
（II）求不等式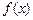≥x2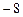
x+15的解集．
（本小题满分10分）选修4-4：坐标系统与参数方程
在平面直角坐标系xOy中，曲线C1的参数方程为
（
为参数），曲线C2的参数方程为
（
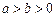，为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=
与C1，C2各有一个交点．当=0时，这两个交点间的距离为2，当=
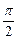时，这两个交点重合．
（I）分别说明C1，C2是什么曲线，并求出a与b的值；
（II）设当=
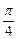时，l与C1，C2的交点分别为A1，B1，当=
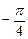时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．
请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分．做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑．
（本小题满分10分）选修4-1：几何证明选讲
如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED．
（I）证明：CD//AB；
（II）延长CD到F，延长DC到G，使得EF=EG，证明：A，B，G，F四点共圆．