(1)(本小题满分7分)
选修4-4:矩阵与变换
已知矩阵
 ,A的一个特征值
,A的一个特征值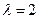 ,其对应的特征向量是
,其对应的特征向量是 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求直线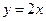 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程
(2)
(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: ,
, 求直线l与曲线C相交所成的弦的弦长.
求直线l与曲线C相交所成的弦的弦长.
((3)(本小题满分7分)
选修4-5:不等式选讲解不等式∣2x-1∣<∣x∣+1
设函数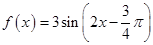 ,(1)求
,(1)求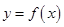 的振幅,周期和初相;(2)求
的振幅,周期和初相;(2)求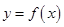 的最大值并求出此时
的最大值并求出此时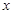 值组成的集合。(3)求
值组成的集合。(3)求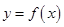 的单调减区间.
的单调减区间.
已知向量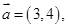

(1)若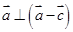 ,求
,求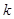 的值;
的值;
(2)若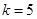 ,
,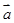 与
与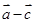 所成的角为
所成的角为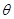 ,求
,求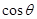
在数列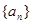 中,
中,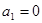 ,且对任意k
,且对任意k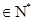 ,
,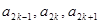 成等差数列,其公差为
成等差数列,其公差为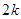 .
.
⑴求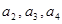 ;
;
⑵求数列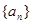 的通项公式;
的通项公式;
⑶记.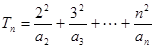 ,证明:
,证明: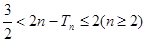 .
.
已知椭圆中心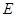 在坐标原点,焦点在
在坐标原点,焦点在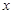 轴上,且经过
轴上,且经过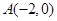 、
、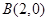 、
、 三点.
三点.
(1)求椭圆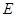 的方程;
的方程;
(2)设直线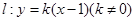 与椭圆
与椭圆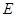 交于
交于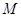 、
、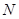 两点.
两点.
①若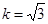 ,求
,求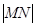 的长;
的长;
②证明:直线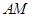 与直线
与直线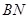 的交点在直线
的交点在直线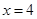 上.
上.
一校办服装厂花费2万元购买某品牌运动装的生产与销售权.根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产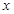 (百套)的销售额
(百套)的销售额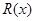 (万元)满足:
(万元)满足:
(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时,利润是多少万元?