直线CD是某电场中的一条电场线,若将一电子从A点处静止释放,电子沿电场线从A到B运动过程中的速度随时间变化的图线如图所示。则A、B两点的电势φA、φB的高低、场强EA、EB及电子在A、B两点的电势能εA、εB的大小关系是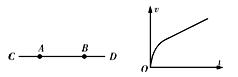
A.εA>εB;EA>EB B.φA>φB;EA>EB
C.εA<εB;EA<EB D.φA<φB;EA<EB
如图8-6所示,两个质量均为m的完全相同的金属球壳a与b,其壳层的厚度和质量分布均匀,将它们固定于绝缘支座上,两球心间的距离为l,为球半径的3倍。若使它们带上等量异种电荷,使其电量的绝对值均为Q,那么,a、b两球之间的万有引力F引库仑力F库分别为: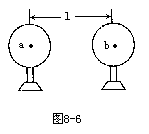
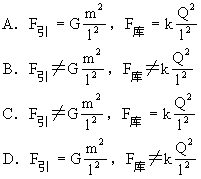
点电荷A和B,分别带正电和负电,电量分别为4Q和Q,在AB连线上,如图8-2,电场强度为零的地方在[ ]
| A.A和B之间 | B.A右侧 |
| C.B左侧 | D.A的右侧及B的左侧 |
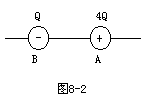
已知理想气体的内能与温度成正比。如图所示的实线汽缸内一定质量的理想气体由状态1到状态2的变化曲线,则在整个过程中汽缸内气体的内能()
| A. | 先增大后减小 | B. | 先减小后增大 |
| C. | 单调变化 | D. | 保持不变 |
如图所示是一列简谐横波在某时刻的波形图,已知图中 位置的质点起振比 位置的质点晚 , 和 之间的距离是 ,则此列波的波长和频率应分别为()
| A. | , | B. | , | C. | , | D. | , |

为研究影响家用保温瓶保温效果的因素,某同学在保温瓶中灌入热水,现测量初始水温,经过一段时间后再测量末态水温。改变实验条件,
先后共做了6次实验,实验数据记录如下表:
| 序号 |
瓶内水量(mL) |
初始水温(0C) |
时间(h) |
末态水温(0C) |
| 1 |
1000 |
91 |
4 |
78 |
| 2 |
1000 |
98 |
8 |
74 |
| 3 |
1500 |
91 |
4 |
80 |
| 4 |
1500 |
98 |
10 |
75 |
| 5 |
2000 |
91 |
4 |
82 |
| 6 |
2000 |
98 |
12 |
77 |
下列眼镜方案中符合控制变量方法的是
A.若研究瓶内水量与保温效果的关系,可用第1、3、5次实验数据
B.若研究瓶内水量与保温效果的关系,可用第2、4、6次实验数据
C.若研究初始水温与保温效果的关系,可用第1、2、3次实验数据
D.若研究保温时间与保温效果的关系,可用第4、5、6次实验数据