如图所示,水平路面CD的左侧有一固定的平台,平台上表面AB长s=3m.光滑半圆轨道AFE竖直固定在平台上,圆轨道半径R=0.4m,最低点与平台AB相切于 A.板长L1=2m,上表面与平台等高,小物块放在板的最右端,并随板一起向平台运动.当板的左端距离平台L=2m时,板与物块向左运动的速度v0=8m/s.当板与平台的竖直墙壁碰撞后,板立即停止运动,物块在板上滑动.已知板与路面的动摩擦因数μ1=0.05,物块与板上表面及轨道AB的动摩擦因数μ2=0.1,物块质量m=1kg,取g=10m/s2.
(1)求物块进入圆轨道时对轨道上A点的压力;
(2)判断物块能否到达圆轨道的最高点E.如果能,求物块离开E后在平台上的落点到A的距离;如果不能,则说明理由.
一灵敏电流计,允许通过的最大电流(满偏电流)为Ig=50μA,表头电阻Rg=1kΩ,若改装成量程为Im=1mA的电流表,应并联的电阻阻值为Ω.若将改装后的电流表再改装成量程为Um=10V的电压表,应再串联一个阻值为Ω的电阻.
为测量阻值约15Q电阻的准确值,实验室现提供以下器材
A.待测电阻RX
B.电流表A1(0~10mA,内阻约2 )
)
C电流表A 2 (0~0.6A,内阻约0.05 )
)
D.电压表V1(0~100mv,内阻约15K )
)
E.屯压表V2(0~5V,内阻约15K )
)
F.定值电阻R定 (约20 )
)
G.滑动变阻器(0~5 ,2A)
,2A)
H.蓄电池(6V,0.5Q)
I.单刀开关两只,导线若干
实验过程中,要求测量时只能测两组数据(U1、I1和U2I2,且无系统误差.
(1)(5分)在方框图中画出测量电路图,并将所选器材用题给符号标在图中;
(2)(3分)R。的表达式为:RX=:(用U1,I1和U2 I2(表示)
(3)(2分)在实物图上用实线代表导线,连接成实验电路.
在“用单摆测定重力加速度”的实验中:
(1)(2分)一位同学用20等分刻度的游标卡尺测摆球的直径,测得的结果如图所示,则摆
球的直径D=cm.
(2)(2分)另一位同学测定了单摆40次全振动的时间如图中秒表所示,那么秒表读数
是,单摆的摆动周期是.
(3)(2分)若测得的g值比当地的标准值偏小,你认为可能的原因是
(写其中一条即可).
青岛奥运会帆船赛场采用风力发电给蓄电池充电,为路灯提供电能。用光敏电阻作为传感器控制路灯电路的开关,实现自动控制。光敏电阻的阻值随照射光的强弱而变化,作为简化模型,可以近似认为,照射光较强(如白天)时电阻几乎为0:照射光较弱(如黑天)时电阻接近于无穷大。利用光敏电阻作为传感器,借助电磁开关,可以实现路灯自动在白天关闭,黑天打开。电磁开关的内部结构如图所示。1、2两接线柱之间是励磁线圈,3、4两接线柱分别与弹簧片和触点连接。当励磁线圈中电流大于50
时,电磁铁吸合铁片,弹簧片和触点分离,3、4断开;电流小于50
时,3、4接通。励磁线圈中允许通过的最大电流为100
。
(1)利用以下器材设计一个自动控制路灯的电路,画出电路原理图。光敏电阻
,符号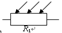 ,灯泡
,额定功率40
,额定电压36
,符号
,灯泡
,额定功率40
,额定电压36
,符号 保护电阻
,符号,
保护电阻
,符号, ,电磁开关,符号
,电磁开关,符号 ,蓄电池
,电压36
,内阻很小;开关
,导线若干。
,蓄电池
,电压36
,内阻很小;开关
,导线若干。
(2)回答下列问题:
①如果励磁线圈的电阻为200
,励磁线圈允许加的最大电压为
,保护电阻
的阻值范围为
。
②在有些应用电磁开关的场合,为了安全,往往需要在电磁铁吸合铁片时,接线柱3、4之间从断开变为接通。为此,电磁开关内部结构应如何改造?请结合本题中电磁开关内部结构图说明。
答:。
③任意举出一个其它的电磁铁应用的例子。
答:。
如图在实验“探索弹力与弹簧伸长的关系”中,某同学根据实验得到的数据描点如图5-5-8所示,其中ΔL表示弹簧的伸长,F表示弹力,请你回答下列问题:
(1)在图558中作出FΔL图象;
(2)由图象得到弹簧的劲度系数k=___________;
(3)求当ΔL="2" cm时弹簧的弹性势能.