（本小题满分13分）已知椭圆的中心在原点，一个焦点F1(0，－2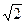
)，且离心率e满足：
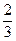，e，
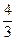成等比数列．
(1)求椭圆方程；
(2)是否存在直线l，使l与椭圆交于不同的两点M、N，且线段MN恰被直线x＝－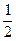
平分．若存在，
求出l的倾斜角的范围；若不存在，请说明理由．
．（本小题满分12分）
已知在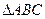
中，a，b，c分别是角A，B，C所对的边，且满足
（I）求角A的大小；
（II）若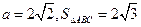
，求b，c的长。
（本小题满分12分）
已知数列
满足
（I）求
的取值范围；
（II）是否存在
，使得
？证明你的结论。
（本小题
满分12分）
如图，双曲线
与抛物线
相交于
，直线AC、BD的交点为P（0，p）。
（I）试用m表示
（II）当m变化时，求p的取值范围。
（本小题满分12分）
已知函数
（I）当a=1时，求
的最小值；
（II）求证：在区间（0，1
）单调递减。
（本小题满分12分）
如图，在正四棱柱ABCD—A1B1C1D1中，AB=1，AA1=2，E为棱AA1上一点，且
平面BDE。
（I）求直线BD1与平面BDE所成角的正弦值；
（II）求二面角C—BE—D的余弦值。