如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4) ,连接AE、ED.
(1)求经过A、E、D三点的抛物线的解析式;
(2)以原点为位似中心,将五边形ABCDE放大.
① 若放大后的五边形的边长是原五边形对应边长的 2 倍,请在网格中画出放大后的五边形A2B2C2D2E2,并直接写出经过A2、E2、D2三点的抛物线的解析式: ;
② 若放大后的五边形的边长是原五边形对应边长的 k 倍,请你直接写出经过Ak、Ek、Dk三点的抛物线的解析式: .(用含k的字母表示)
如图,水池中有水,水面是一个边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度和这根芦苇的长度分别是多少?
如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积.
如图,已知点B、C、D在同一条直线上,△ABC和△ECD均是等边三角形.BE与AC交于点H,AD与CE交于点G.
(1)求证:△BCE≌△ACD;
(2)判断GH与BD的位置关系,并证明.
李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
如图所示,已知点A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.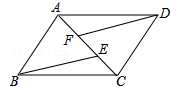
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.