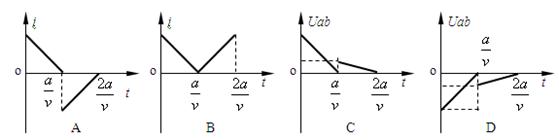
如右图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的 ( )
伽利略创造的把实验、假设和逻辑推理相结合的科学方法,有力地促进了人类科学认识的发展。利用如图所示的装置做如下实验:小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升。斜面上先后铺垫三种粗糙程度逐渐减低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3。根据三次实验结果的对比,可以得到的最直接的结论是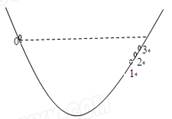
| A.如果斜面光滑,小球将上升到与O点等高的位置 |
| B.如果小球不受力,它将一直保持匀速运动或静止状态 |
| C.如果小球受到力的作用,它的运动状态将发生改变 |
| D.小球受到的力一定时,质量越大,它的加速度越小 |
下列说法正确的是()
| A.若物体运动速率始终不变,则物体所受合力一定为零 |
| B.若物体的加速度均匀增加,则物体做匀加速直线运动 |
| C.若物体所受合力与其速度方向相反,则物体做匀减速直线运动 |
| D.若物体在任意的相等时间间隔内位移相等,则物体做匀速直线运动 |
(多选)如图所示,竖直放置的轻弹簧的一端固定在地面上,另一端与斜面体P连接,P与斜放的固定挡板MN接触且处于静止状态,弹簧处于竖直方向,则斜面体P此刻受到外力的个数可能为( )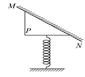
| A.2个 | B.3个 | C.4个 | D.5个 |
(多选)如图所示,质量为m的物体在与斜面平行向上的拉力F作用下,沿着水平地面上质量为M的粗糙斜面匀速上滑,在此过程中斜面保持静止,则地面对斜面( )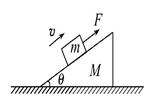
| A.无摩擦力 |
| B.支持力等于(m+M)g |
| C.支持力为(M+m)g-Fsinθ |
| D.有水平向左的摩擦力,大小为Fcosθ |
(单选)如图所示,在水平天花板的A点处固定一根轻杆a,杆与天花板保持垂直。杆的下端有一个轻滑轮O。另一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,BO段细线与天花板的夹角θ=30°。系统保持静止,不计一切摩擦。下列说法中正确的是( )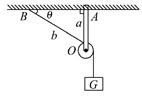
A.细线BO对天花板的拉力大小是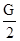 |
B.a杆对滑轮的作用力大小是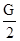 |
| C.a杆和细线对滑轮的合力大小是G |
| D.a杆对滑轮的作用力大小是G |