如图所示,纸平面内O点有一离子源,不断向纸面内各个方向放出离子,已知离子速度V=5X106m/s,荷质比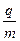 =2X107C/kg。空间中存在以粒子源为圆心垂直于纸面向里半径R1=0.5m的匀强磁场B1,在这个磁场外面还存在着以粒子源为圆心垂直于纸面向外的圆环形匀强磁场B2,外径为R2,B1= B2=0.5T,(设粒子在运动过程中不相
=2X107C/kg。空间中存在以粒子源为圆心垂直于纸面向里半径R1=0.5m的匀强磁场B1,在这个磁场外面还存在着以粒子源为圆心垂直于纸面向外的圆环形匀强磁场B2,外径为R2,B1= B2=0.5T,(设粒子在运动过程中不相 撞,忽略重力和粒子间的相互作用)求:
撞,忽略重力和粒子间的相互作用)求:
(1)粒子在B1中运动时的轨道半径为多少
(2)为了使粒子不离开磁场区域,R2的最小值
(3)求粒子从O点出发再回到O点的最短时间。
如图所示,一个载货小车总质量为50kg,静止在水平地面上,现用大小为300N,跟水平方向成30°角斜向上的拉力拉动货车,做匀加速运动4s后撤去拉力,再经5s车的速度多大?货车运动的总位移是多少?(已知μ=0.1, g=10m/s2
如图所示,一质量为M=5.0kg的平板车静止在光滑水平地面上,平板车的上表面距离地面高h=0.8m,其右侧足够远处有一固定障碍物A.另一质量为m=2.0kg可视为质点的滑块,以v0=8m/s的水平初速度从左端滑上平板车,同时对平板车施加一水平向右、大小为5N的恒力F.当滑块运动到平板车的最右端时,两者恰好相对静止.此时车去恒力F.此后当平板车碰到障碍物A时立即停止运动,滑块水平飞离平板车后,恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道,并沿轨道下滑.已知滑块与平板车间的动摩擦因数μ=0.5,圆弧半径为R=1.0m,圆弧所对的圆心角∠BOD=θ=1060,g取10m/s2,sin530=0.8,cos530=0.6,不计空气阻力,求: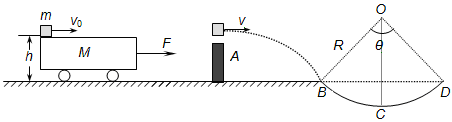
(1)平板车的长度;
(2)障碍物A与圆弧左端B的水平距离;
(3)滑块运动圆弧轨道最低点C时对轨道压力的大小.
如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=370,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T.求(取g=10m/s2,结果可用根式表示):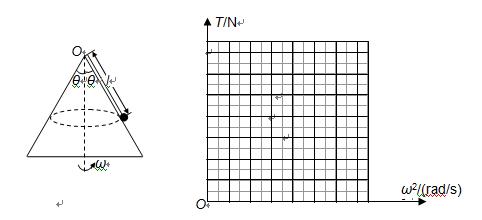
若要小球离开锥面,则小球的角速度ω0至少为多大?
若细线与竖直方向的夹角为600,则小球的角速度ω'为多大?
细线的张力T与小球匀速转动的加速度ω有关,请在坐标纸上画出ω的取值
范围在0到ω'之间时的T—ω2的图象(要求标明关键点的坐标值).
)频闪照相是研究物理过程的重要手段,如图是某同学研究小滑块从光滑水平面滑上粗糙斜面并向上滑动时的频闪照片.已知斜面足够长,倾角α=370,闪光频率10Hz.经测量换算获得实景数据:sl=s2=40cm,s3=35cm,s4=25cm,s5=15cm,取g=l0m/s2,sin370=0.6,cos370=0.8.设滑块通过平面与斜面连接处时没有能量损失,求: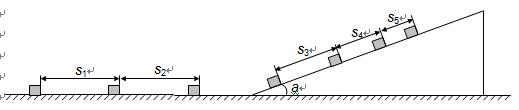
滑块与斜面间的动摩擦因数μ;
滑块从滑上斜面到返回斜面底端所用的时间.
如图所示,长为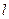 的细线一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直平面内做完整的圆周运动,已知O点到水平地面的距离Soc =L且 L>
的细线一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直平面内做完整的圆周运动,已知O点到水平地面的距离Soc =L且 L>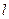 ,重力加速度为g
,重力加速度为g
求小球通过最高点A时的速度vA的大小.
求小球通过最低点B时,细线对小球的拉力.
求小球运动到A点或B点时细线断裂,小球落到地面对到C点的距离若相等,则
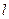 和L应满足什么关系?
和L应满足什么关系?