一种自行车车头灯如图7，是通过自行车带动小型发电机供电的。图8是这种发电机结构示意图。图中转轴的一端装有一对随轴转动的磁极，另一端装有一半径r0＝1.0cm的摩擦小轮。电枢线圈绕在固定的U形铁心上，设线框N＝800匝，线圈的横截面积S＝20cm2，旋转磁极的磁感强度B＝0.010T。
自行车车轮的半径R1＝35cm，车头灯的电阻为10Ω，线圈总电阻40Ω，车头灯正常工作时的电流为60~70mA。当自行车车轮转动的角速度为8rad/s时，车头灯是否能正常工作？（假定摩擦小轮与自行车轮之间无相对滑动）
某人站在离地20m平台边缘，以20m/s的初速度竖直向上抛出一石块，不考虑空气阻力，g=10m/s2，求：
（1）物体上升的最大高度是多少？回到抛出点的时间是多少？
（2）石块从抛出回到地面所需的时间是多少？落到地面的速度是多少？
在航天事业中要用角速度计可测得航天器自转的角速度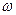
，其结构如图所示，当系统绕OO/转动时，元件A在光滑杆上发生滑动，并输出电信号成为航天器的制导信号源。已知A质量为m，弹簧的劲度系数为k，原长为L0，电源电动势为E，内阻不计，滑动变阻器总长为L，电阻分布均匀，系统静止时滑动变阻器触头P在中点，与固定接头Q正对，当系统以角速度
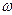转动时，求：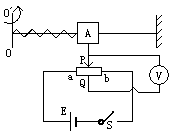
（1）弹簧形变量x与
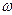的关系式；
（2）电压表的示数U与角速度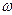的关系式
根据如图所示的振动图象：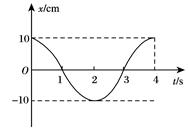
(1)算
出下列时刻振子对平衡位置的位移.
①t1="0.5" s;②t2=1.
5s.
(2)将位移时间的变化规律写成x=Asin(ωt+φ)的
形式并指出振动的初相位.
如图所示，在连有电阻R=3r的裸铜线框ABCD上，以AD为对称轴放置另一个正方形的小裸铜线框abcd，整个小线框处于垂直框面向里、磁感强度为B的匀强磁场中．已知
小线框每边长L，每边电阻为r,其它电阻不计。现使小线框以速度v向右平移，求通过电阻R的电流及R两端的电压．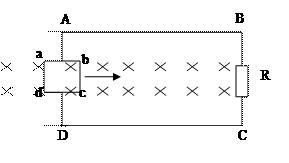
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行
周期T。