如图所示，在匀强电场中有一半径为R的圆o，场强方向与圆o所在平面平行，场强大小为为E，电荷量为q的带正电微粒以相同的初动能沿着各个方向从A点进入圆形区域中，只在电场力作用下运动，从圆周上不同点离开圆形区域，其中从C点离开圆形区域的带电微粒的动能最大，图中0是圆心，AB是圆的直径,AC是与AB成a角的弦，则( )
| A．匀强电场的方向沿AC方向 |
| B．匀强电场的方向沿CO方向 |
C．从A到c电场力做功为 |
D．从A到c电场力做功为 |
一个静止的质点，在0～5s时间内受到力F的作用，力的方向始终在同一直线上，力F 随时间t的变化图线如图所示。则质点在 ( )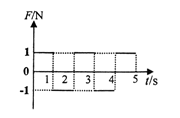
| A．第2 S末速度方向改变 |
| B．第2 s末速度为负值 |
| C．第4 S末运动速度为零 |
| D．第4 s末回到原出发点 |
有一种“傻瓜”相机的曝光时间(快门从打开到关闭的时间)是固定不变的。为了估测相机的曝光时间，有位同学提出了下述实验方案：如图1，他从墙面上A点的正上方与A相距H="1.5" m处，让一个小石子自由落下，在小石子下落通过A点的同时按动快门对小石子照相，得到如图所示的照片。由于小石子的运动，它在照片上留下一条模糊的径迹CD。已知每块砖的平均厚度约为6cm，
取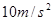
。从这些信息估算相机的曝光时间最接近的值是（）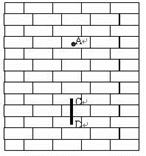
| A．0.5 s | B．0.06 s | C．0.02 s | D．0.008 s |
如图甲所示，一轻杆一端固定在O点，另一端固定一小球，在竖直平面内做半径为R的圆周运动。小球运动到最高点时，杆与小球间弹力大小为N，小球在最高点的速度大小为v，N-v2图像如乙图所示。下列说法正确的是
A．当地的重力加速度大小为 |
B．小球的质量为 |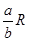
| C．v2=c时，杆对小球弹力方向向上 |
| D．若c=2b，则杆对小球弹力大小为2a |
如图，在水平板的左端有一固定挡板，挡板上连接一轻质弹簧。紧贴弹簧放一质量为m的滑块，此时弹簧处于自然长度。已知滑块与板的动摩擦因数为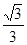
，最大静摩擦力等于滑动摩擦力。现将板的右端缓慢抬起（板与水平面的夹角为θ），直到板竖直，此过程中弹簧弹力的大小F随夹角θ的变化关系可能是
一个高尔夫球静止于平坦的地面上，在t=0时球被击出，飞行中球的速率与时间的关系如图所示。若不计空气阻力的影响，根据图象提供的信息可以求出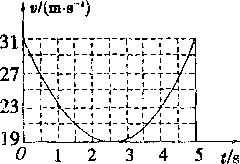
| A．高尔夫球在何时落地 |
| B．高尔夫球可上升的最大高度 |
| C．人击球时对高尔夫球做的功 |
| D．高尔夫球落地时离击球点的距离 |