(
某篮球联赛的总决赛在甲、乙两队之间角逐。采用七场四胜制,即有一队胜四场,则此队获胜,
同时比赛结束。在每场比赛中,两队获胜的概率相等。根据以往资料统计,每场比赛组织者可获
门票收入32万元,两队决出胜负后,问:
(1)组织者在此次决赛中,获门票收入为128万元的概率是多少?
(2)设组织者在此次决赛中获门票收入为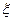 ,求
,求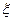 的分布列及
的分布列及 。
。
如图,在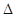 ABC中,G为中线AM为中点,O为
ABC中,G为中线AM为中点,O为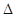 ABC外一点,若
ABC外一点,若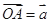 ,
, ,
, ,求
,求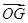 (用
(用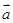 、
、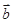 、
、 表示)
表示)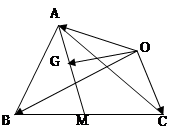
在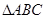 中,角
中,角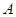 ,
,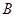 ,
, 所对的边分别是
所对的边分别是 ,
,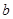 ,
, ,且满足
,且满足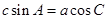 .
.
(1)求角 的大小;
的大小;
(2)求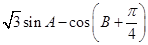 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角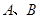 的大小.
的大小.
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为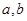 .
.
(1)求直线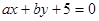 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求 的概率.
的概率.
已知函数
(1)在给定的平面直角坐标系中,画函数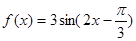 ,
, 的简图;
的简图;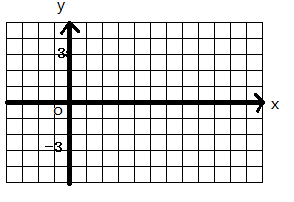
(2)求
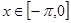 的单调增区间;
的单调增区间;
(3) 函数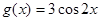 的图象只经过怎样的平移变换就可得到
的图象只经过怎样的平移变换就可得到 的图象?
的图象?