如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2)当直线 与△ABC有交点时,b的取值范围是()
与△ABC有交点时,b的取值范围是()
| A.-1≤b≤1 | B.- ≤ ≤ ≤1 ≤1 |
C.- ≤ ≤ ≤ ≤ |
D.-1≤ ≤ ≤ |
如图,在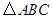 中,
中,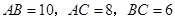 ,经过点
,经过点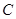 且与边
且与边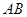 相切的动圆与
相切的动圆与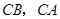 分别相交于点
分别相交于点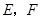 ,则线段
,则线段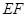 长度的最小值是()
长度的最小值是()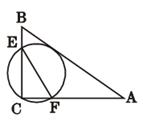
A.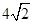 |
B.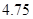 |
C.4.8 | D.5 |
如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()
| A.3 | B.4 | C.5 | D.6 |
如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD= CD•OA;⑤∠DOC=90°,其中正确的个数共有()
CD•OA;⑤∠DOC=90°,其中正确的个数共有()
A.1个 B.2个 C.3个 D.4个
已知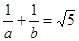
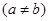 ,则
,则
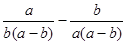 的值为()
的值为()
A.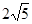 |
B.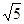 |
C.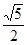 |
D.1 |