半径为R的水平圆台，可绕通过圆心O的竖直光滑细轴CC′转动，如图所示，圆台上沿相互垂直的两个半径方向刻有凹槽，质量为mA的物体A放在一个槽内，物体A与槽底间的动摩擦因数为μ，质量为mB的物体B放在另一个槽内，此槽是光滑的．AB间用一长为l（l<R）且不可伸长的轻绳绕过细轴相连．已知圆台做匀速转动，且A、B两物体相对圆台不动（A、B两物体可视为质点，物体的最大静摩擦力近似等于滑动摩擦力）．
（1）当圆台转动的角速度为ω0，OA的长度为l1时，试写出A、B两个物体受到的向心力大小的表达式．
（2）不论圆台转动的角速度为多大，要使物体A和槽之间恰好没有摩擦力，则OA的长为多大？
（3）设OA长为x，试分析圆台的角速度ω和物体A到圆心的距离x所应满足的条件．
如图所示，轻弹簧的两端与质量均为2m的B、C两物块固定连接，静止在光滑水平面上，物块C紧靠挡板但不粘连．另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰，碰撞时间极短可忽略不计．（所有过程都在弹簧弹性限度范围内）求：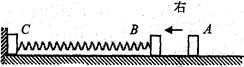
（1）A、B碰后瞬间各自的速度；
（2）弹簧第一次压缩最短与第一次伸长最长时弹性势能之比．
A、B为竖直墙壁上等高的两点，AO、BO为长度相等的两根轻绳，CO为一根轻杆。转轴C在AB中点D的正下方，AOB在同一水平面上。∠AOB=90º，∠COD=60º。若在O点处用轻绳悬挂一个质量为m的物体，求平衡后绳AO所受拉力的大小。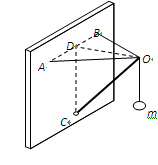
光滑水平面上放着质量mA=1kg的物块A与质量mB=2kg的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，用手挡住B不动，此时弹簧弹性势能Ep=49J。如图所示，放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R=0.5m，B恰能到达最高点C取g=10m/s2，求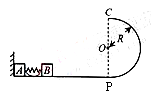
（1）B落地点距P点的距离（墙与P点的距离很远）
（2）绳拉断后瞬间B的速度vB的大小
（3） 绳拉断过程绳对A所做的功W．
如图所示，一电子（其重力不计，质量为m、电荷量为e，由静止开始，经加速电场加速后，水平向右从两板正中间射入偏转电场．偏转电场由两块水平平行放置的长为l相距为d的导体板组成，当两板不带电时，电子通过两板之间的时间均为t0，当在两板间加电压为U0时，电子可射出偏转电场，并射入垂直纸面向里的匀强磁场，最后打在磁场右侧竖直放置的荧光屏上．磁场的水平宽度为s，竖直高度足够大。求：
（1）加速电场的电压；
（2）电子在离开偏转电场时的侧向位移；
（3）要使电子能垂直打在荧光屏上，匀强磁场的磁感应强度为多大？
如图所示，将直径为2R的半圆形导轨固定在竖直面内的A、B两点，直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环，原长为2R、劲度系数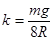
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律，形变量相同时弹性势能也相等，且弹性绳始终在弹性限度内，重力加速度为g，不计一切摩擦。将圆环由A点正下方的C点静止释放，当圆环运动到导轨的最低点D点时，求
（1）圆环的速率v；
（2）导轨对圆环的作用力F的大小?