((本小题满分14分)
已知圆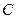 的圆心为
的圆心为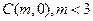 ,半径为
,半径为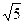 ,圆
,圆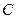 与椭圆
与椭圆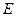 :
: 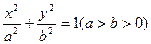 有一个公共点
有一个公共点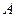 (3,1),
(3,1),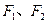 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆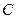 的标准方程;
的标准方程;
(2)若点P的坐标为(4,4),试探究斜率为k的直线
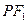 与圆
与圆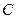 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆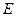 和直线
和直线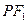 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
叙述并证明余弦定理.
设椭圆
过点
,离心率为
.
(Ⅰ)求
的方程;
(Ⅱ)求过点
且斜率为
的直线被
所截线段的中点坐标.
如图,在 中, , , 是 上的高,沿 把是 上的 折起,使 .

(Ⅰ)证明:平面
平面
;
(Ⅱ)设
,求三棱锥
的表面积.
平面内与两定点
,
(
)连线的斜率之积等于非零常数
的点的轨迹,加上
两点所成的曲线
可以是圆、椭圆成双曲线.
(Ⅰ)求曲线
的方程,并讨论
的形状与
值的关系;
(Ⅱ)当
=﹣1时,对应的曲线为
;对给定的
∈(﹣1,0)∪(0,+∞),对应的曲线为
,设
是
的两个焦点.试问:在
上,是否存在点
,使得
的面积
.若存在,求
的值;若不存在,请说明理由.
设函数
,其中
,
为常数,已知曲线
与
在点
处有相同的切线
.
(Ⅰ)求
的值,并写出切线
的方程;
(Ⅱ)若方程
有三个互不相同的实根
,其中
,且对任意的
恒成立,求实数
的取值范围.