如图9，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1, －3）．
（1）求抛物线的解析式；
（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；
（3）在第（2）问的结论下，抛物线上的点P使S△PAD＝4S△ABM成立，求点P坐标．
如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，若AB=17，BD=12，
（1）求证：△BCD≌△ACE；
（2）求DE的长度．
如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．
求证：△ACD≌△BCE．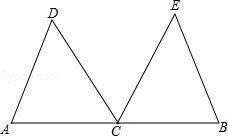
如图，已知：AB=CB，AD=CD，求证：∠A=∠C．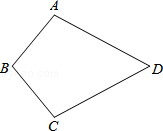
求下列各式中的x：
（1）4x2=81；
（2）（x﹣1）3=64．
如图，长方形纸片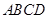
中，AB=10，将纸片折叠，使顶点
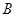落在边
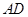上的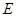
点处，折痕的一端
点在边
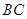上．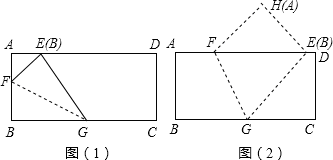
（1）如图（1），当折痕的另一端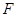
在
边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端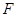在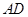边上且BG=13时，求AF的长．