(本小题满分12分)
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =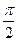 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(I)当x=2时,求证:BD⊥EG ;
(II)若以F、B、C、D为顶点的三棱锥的体积记为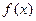 ,
,
求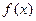 的最大值;
的最大值;
(III)当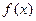 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.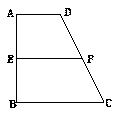
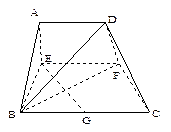 ]
]
计算下列定积分
(1) (2)
(2)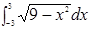
(本题满分10分)
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 (Ⅰ)求证:平面BEF⊥平面ABC;(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
(Ⅰ)求证:平面BEF⊥平面ABC;(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
(本题满分10分)
已知三角形的三个顶点是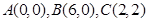 .
.
(1)求 边上的高所在直线的方程.
边上的高所在直线的方程.
(2)设三角形两边 的中点分别为
的中点分别为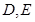 ,试用坐标法证明:
,试用坐标法证明: ∥
∥ 且
且 .
.
.(本小题10分)
如图,在四棱锥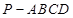 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
,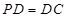 .
. 是
是 的中点.(1)证明
的中点.(1)证明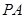 ∥平面
∥平面 ;(2)证明:
;(2)证明: ⊥平面
⊥平面 .
.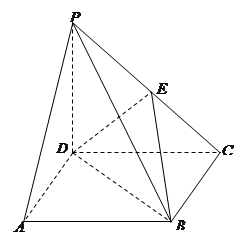
(本小题10分)求经过两直线3x + 4y – 5 = 0与2x – 3y + 8 = 0的交点M,且与直线L1:2x + y + 5 = 0平行的直线L2的方程,并求L1与L2间的距离。