如图15所示,水平桌面上有一轻弹簧,左端固定在A点,弹簧处于自然状态时其右端位于B点.水平桌面右侧有一竖直放置的光滑圆弧形轨道MNP,其半径R=0.8 m,OM为水平半径,ON为竖直半径,P点到桌面的竖直距离也是R,∠PON=45°第一次用质量m1=1.1 kg的物块(可视为质点)将弹簧缓慢压缩到C点,释放后物块停在B点(B点为弹簧原长位置),第二次用同种材料、质量为m2=0.1 kg的物块将弹簧也缓慢压缩到C点释放,物块过B点后做匀减速直线运动,其位移与时间的关系为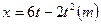 ,物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道.(g=10 m/s2,不计空气阻力)
,物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道.(g=10 m/s2,不计空气阻力)
求:(1)BC间的距离;
(2)m2由B运动到D所用时间;
(3)物块m2运动到M点时,m2对轨道的压力.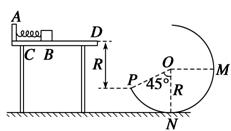
如图所示,从A点以v0=4m/s的水平速度抛出一质量m=lkg的小物块(可视为质点),当物块运动至B点时,恰好沿切线方向进入光滑圆弧轨道BC,经圆孤轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平。已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,R=0.75m,物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2。g取10m/s2,求:
(1)小物块运动至B点时的速度大小和方向;
(2)小物块滑动至C点时,对圆弧轨道C点的压力;
(3)长木板至少为多长,才能保证小物块不滑出长木板?
倾角为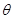 的光滑斜面上,一劲度系数为k的轻弹簧连接质量分别为m1、m2的甲、乙两小物块.开始时,两物块在光滑挡板作用下静止在斜面上.现作用在乙物块一平行于斜面向上的力,使乙物块以加速度a匀加速运动.问
的光滑斜面上,一劲度系数为k的轻弹簧连接质量分别为m1、m2的甲、乙两小物块.开始时,两物块在光滑挡板作用下静止在斜面上.现作用在乙物块一平行于斜面向上的力,使乙物块以加速度a匀加速运动.问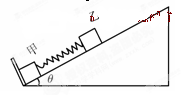
(1)经多长时间物块甲离开挡板?
(2)从开始到物块甲恰好离开挡板的过程中,作用在乙物块上的力的最大值和最小值分别是多大?
如图甲所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定,下端悬空,为了研究学生沿杆的下滑情况,在杆的顶部装有一拉力传感器,可显示杆顶端所受拉力的大小,现有一学生(可视为质点)从上端由静止开始滑下,5s末滑到杆底端时速度恰好为零并静止悬挂在杆的底端.从学生开始下滑时刻计时,传感器显示拉力随时间变化情况如图乙所示,g取10m/s2,求:
(1)该学生下滑过程中的最大速率;
(2)图中力F1的大小;
(3)滑杆的长度.
一辆客车在平直公路上以30m/s的速度行驶,突然发现正前方46m处有一货车正以20m/s的速度沿同一方向匀速行驶,于是客车司机刹车,以2m/s2的加速度做匀减速直线运动,又知客车司机的反应时间为0.6s(司机从发现货车到采取制动措施经历的时间).问此后的过程中客车能否会撞到货车上?
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,
(1)A轮每秒的转数n最少是多少?
(2)若A轮有上述的最小转速,且其最高点距地面高度为h,求小物体落地的速度方向(用反三角函数表示)