如图甲所示，宽度为d的竖直狭长区域 内(边界为L1、L2)，存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图7乙所示)，电场强度的大小为E0，E>0表示电场方向竖直向上．t＝0时，一带正电、质量为m的尘埃从左边界上的N1点以水平速度v射入该区域，沿直线运动到Q点后，做一次完整的圆周运动，再沿直线运动到右边界上的N2点．Q为线段N1N2的中点,重力加速度为g.上述d、E0、m、v、g为已知量．
(1)求微粒所带电荷量q和磁感应强度B的大小；
(2)求电场变化的周期T；
(3)改变宽度d，使微粒仍能按上述运动过程通过相应宽度的区域，求T的最小值．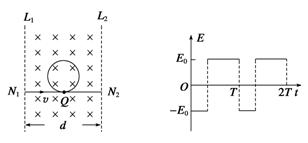
竖直悬挂一根长15m的杆，在杆的正下方距杆下端5m处有一观察点A，当杆自由下落时，杆全部通过A点需多长时间？（g取10m/s2）
一辆卡车初速度为10m/s，以a=2m/s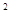
的加速度做匀加速直线运动，求：
（1）卡车在第6s末的速度多大?
（2）卡车在前6s内的位移多大?
（3）卡车在前6s内的平均速度多大?
（4）卡车在第6s内的位移多大?
质量M＝9kg、长L=1m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行，当速度v0=2m/s时，在木板的右端轻放一质量m=1kg的小物块如图所示．当小物块刚好滑到木板左端时，物块和木板达到共同速度。取g=10m/s2，求：
（1）从物块放到木板上到它们达到共同速度所用的时间t.
（2）小物块与木板间的摩擦因数μ2。
（3）物块从放上木板到停下来经过的位移。
如图所示，质量m=2.0kg的木块静止在高h=1.8m的水平平台上，木块距平台右边缘d=7.75m，木块与平台间的动摩擦因数μ=0.2．用F=20N的水平拉力拉木块，木块向右运动s1=4.0m时撤去F．不计空气阻力，g取10m/s2．求：
（1）F作用于木块的时间；
（2）木块离开平台时的速度大小；
如图所示，拉杆箱是由拉杆和箱子构成的交通旅游工具．设箱子的质量为m，拉杆质量可忽略．箱子与水平地面之间的动摩擦因数为常数μ，重力加速度为g．某同学在水平地面上拉动拉杆箱，设拉力的方向沿拉杆方向，拉杆与水平方向的夹角为θ．
（1）若箱子在水平地面上匀速移动，求拉力的大小；
（2）已知θ存在一临界角θ0，若θ=θ0，则箱子在水平地面上匀速移动时，拉力有最小值，求这一临界角的正切tanθ0和对应的拉力最小值．