若对函数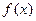 定义域内的任意两个实数
定义域内的任意两个实数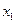 ,
,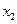 ,满足
,满足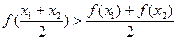 ,则称函数
,则称函数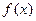 为凸函数.给出下列几个函数:
为凸函数.给出下列几个函数:
① ;②
;②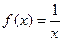 ,
,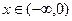 ;③
;③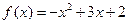 ,
,
④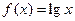 ; ⑤
; ⑤ .
.
其中是凸函数的有
| A.1个 | B.2个 | C.3个 | D.4个 |
设集合 则
则 个数为()
个数为()
| A.3 | B.4 | C.5 | D.6 |
若复数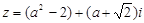 为纯虚数,则
为纯虚数,则 的虚部为()
的虚部为()
A.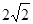 |
B.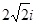 |
C.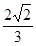 |
D.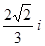 |
在集合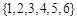 中任取一个偶数
中任取一个偶数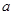 和一个奇数
和一个奇数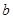 构成以原点为起点的向量
构成以原点为起点的向量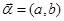 ,从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为
,从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为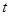 ,在区间
,在区间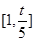 和
和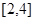 分别各取一个数,记为
分别各取一个数,记为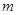 和
和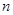 ,则方程
,则方程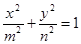 表示焦点在
表示焦点在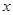 轴上的椭圆的概率是( )
轴上的椭圆的概率是( )
A.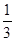 |
B.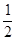 |
C.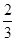 |
D.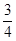 |
已知 是定义
是定义 上的不恒为零的函数,且对于任意实数
上的不恒为零的函数,且对于任意实数 满足:
满足: ,
, ,
, ,
, ,
,
考察下列四个结论: ① ; ②
; ② 为偶函数; ③数列
为偶函数; ③数列 为等比数列;
为等比数列;
④数列 为等差数列。其中正确的结论是( )
为等差数列。其中正确的结论是( )
| A.①③④ | B.①②③ | C.①②④ | D.①④ |
已知双曲线 的右焦点为
的右焦点为 ,若过点
,若过点 且倾斜角为
且倾斜角为 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |