若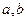 ,
, 表示不同的直线,
表示不同的直线, 表示两个不同的平面,给出如下四组命题:
表示两个不同的平面,给出如下四组命题:
①“直线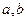 为异面直线”的充分非必要条件是“直线
为异面直线”的充分非必要条件是“直线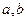 不相交”;
不相交”;
②“ ⊥
⊥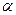 ”的充要条件是“直线
”的充要条件是“直线 垂直于平面
垂直于平面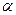 内的无数多条直线”;
内的无数多条直线”;
③“ ∥
∥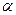 ”的充分非必要条件是“
”的充分非必要条件是“ 上存在两点到
上存在两点到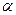 的距离相等”.
的距离相等”.
④“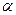 ∥
∥ ”的必要非充分条件是“存在
”的必要非充分条件是“存在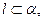
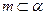 且
且 ∥
∥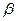 ,
, ∥
∥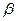 ”.
”.
其中正确的命题是( )
| A.④ | B.③④ | C.①② | D.② |
某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
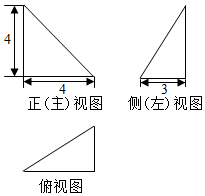
| A. | 8 | B. | C. | 10 | D. |
根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为 ( 为常数)。已知工人组装第4件产品用时30分钟,组装第 件产品用时15分钟,那么 和 的值分别是()
| A. | 75,25 | B. | 75,16 | C. | 60,25 | D. | 60,16 |
如图,
分别与圆
切于点
,延长
与圆
交于另一点
。给出下列三个结论:
①
;
②
③
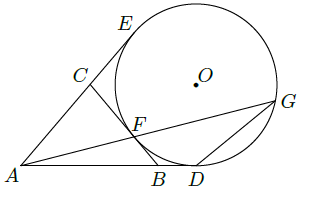
其中正确结论的序号是
| A. | ①② | B. | ②③ |
| C. | ①③ | D. | ①②③ |
执行如图所示的程序框图,输出的 值为( )
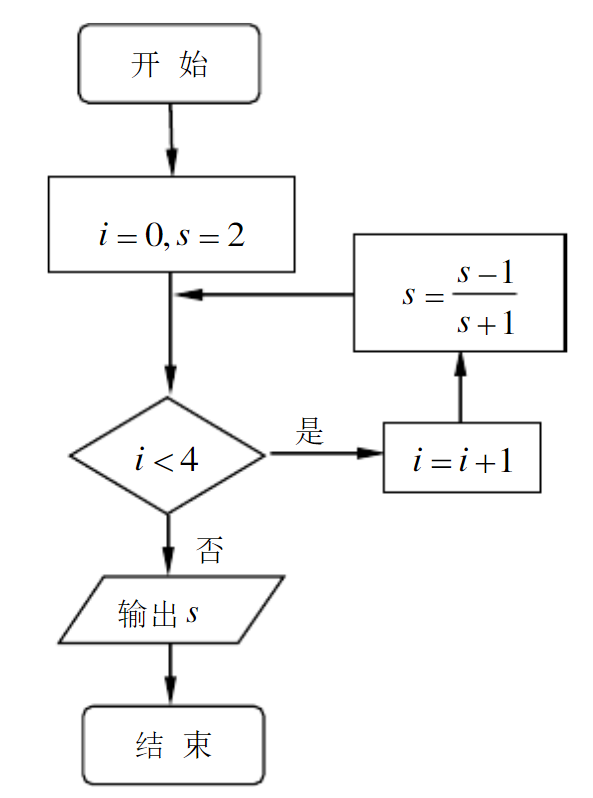
| A. |
|
B. |
|
| C. |
|
D. |
|
在极坐标系中,圆 的圆心的极坐标系是()
| A. | B. | C. | D. |