已知数列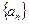 满足
满足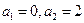 ,且对任意的
,且对任意的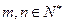 都有
都有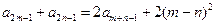

(本小题满分12分)
在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为 和
和 .
.
(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出
的分布列,并求其数学期望.
(本小题满分12分)
如图,三棱柱 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是,D是AC的中点。
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
(本小题满分12分)
已知数列 为等差数列,且
为等差数列,且 .
. 为等比数列,数列
为等比数列,数列 的前三项依次为3,7,13.求
的前三项依次为3,7,13.求
(1)数列 ,
, 的通项公式;
的通项公式;
(2)数列 的前
的前 项和
项和 .
.
设函数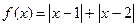 .
.
(1)画出函数y=f(x)的图像;
(2)若不等式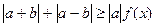 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
已知圆方程为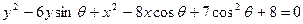 .
.
(1)求圆心轨迹的参数方程C;
(2)点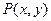 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求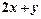 的取值范围.
的取值范围.