如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1.0m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻。匀强磁场方向与导轨平面垂直,质量为0.2kg。电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.求:
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为4W,求该速度的大小;
(3)在上问中,若R=2 W,金属棒中的电流方向由b到a,求磁感应强度的大小与方向(g=10rn/s2,sin37°=0.6, cos37°=0.8)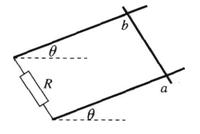
已知在t1时刻简谐横波的波形如图中实线所示,在时刻t2该波的波形如图中虚线所示。t2–t1 = 0.1s。求:
(1)该波可能的传播速度υ1;
(2)若波源的振动周期T满足5T < t2–t1 < 6T,且图中P质点在t1时刻的即时速度方向沿y轴正方向,求波速υ2。
(3)若波源的振动周期T满足0.02s < T < 0.025s,且从t1时刻起,图中Q质点比R质点先回到平衡位置,求波速υ3。
某小型实验水电站输出功率是20kW,输电线总电阻是6Ω。
(1)若采用380V输电,求输电线路损耗的功率;
(2)若改用5000V高压输电,用户端利用n1∶n2 = 22∶1的变压器降压,求用户得到的电压。
(计算结果均保留三个有效数字)
质量为M的木块在水平面上处于静止状态,有一质量为m的子弹以水平速度v0击中木块并与其一起运动,若木块与水平面之间的动摩擦因数为μ,则木块在水平面上滑行的距离为多少?(设子弹与木块作用时间极短)
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目(如图)。2012年8月3日在伦敦奥运会上,我国运动员董栋勇夺金牌。假设一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。求这段时间内网对运动员的平均作用力是多大?(g取10m/s2)
一群氢原子处于量子数n=4的能级状态,氢原子的能级图如图所示,则:
(1)氢原子由量子数n=4的能级跃迁到n=2的能级时辐射光子的能量是多少电子伏?
(2)用(1)中的光子照射下表中几种金属,哪些金属能发生光电效应?发生光电效应时,发射光电子的最大初动能是多大?
| 金属 |
铯 |
钙 |
镁 |
钛 |
| 逸出功W/eV |
1.9 |
2.7 |
3.7 |
4.1 |