(本小题满分12分)
如图,五面体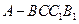 中,
中, .底面
.底面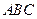 是正三角形,
是正三角形,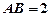 .四边形
.四边形 是矩形,二面角
是矩形,二面角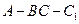 为直二面角.
为直二面角.
(Ⅰ)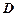 在
在 上运动,当
上运动,当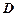 在何处时,有
在何处时,有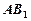 ∥平面
∥平面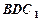 ,
,
并且说明理由;
(Ⅱ)当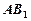 ∥平面
∥平面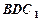 时,求二面角
时,求二面角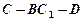 余弦值.
余弦值.
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。
在ΔABC中,角A、B、C所对的边分别为a,b,c,且 ,
, ,
, 。
。
(1)求 的值;
的值;
(2)求ΔABC的面积。
已知平面向量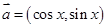 ,
, ,
, ,
, ,
, .
.
(1)当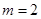 时,求
时,求 的取值范围;
的取值范围;
(2)若 的最大值是
的最大值是 ,求实数
,求实数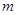 的值;
的值;
(3)(仅理科同学做,文科同学不做)若 的最大值是
的最大值是 ,对任意的
,对任意的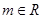 ,都有
,都有 恒成立,求实数
恒成立,求实数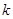 的取值范围.
的取值范围.
已知数列 满足
满足 ,
, ;数列
;数列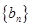 满足
满足 ,
,  .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)求数列 、
、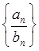 的前
的前 项和
项和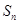 ,
, .
.
设函数 .
.
(1)求函数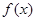 的最小正周期;
的最小正周期;
(2)若 ,且
,且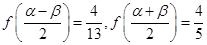 ,求
,求 的值.
的值.