(本小题满分1 2分)
2分)
已知函数 ,函数
,函数 是区间[-1,1]上的减
是区间[-1,1]上的减 函数.
函数.
(I)求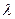 的最大值;
的最大值;
(II)若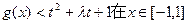 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程 的根的个数.
的根的个数.
(本小题满分13分)
已知数列 的前n项和
的前n项和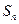 与通项
与通项 之间满足关系
之间满足关系
(I)求数列 的通项公式;
的通项公式;
(II)设 求
求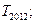
(III)若 ,求
,求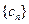 的前n项和
的前n项和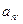
(本小题满分13分)已知函数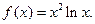
(I)求函数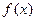 的单调区间;
的单调区间;
(II)若
 ,在(1,2)上为单调递
,在(1,2)上为单调递
减函数。求实数a的范围。
(本小题满分13分)已知椭圆的中心在原点,焦点在y轴上,离心率为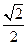 ,且
,且
椭圆经过圆 的圆心C。
的圆心C。
(I)求椭圆的标准方程;
(II)设直线 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点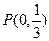 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线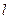 的方程。
的方程。
(本小题满分12分)如图,在多面体ABDEC中,AE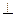 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(I)求证:EF//平面ABC;
(II)求证: 平面BCD;
平面BCD;
(III)求多面体ABDEC的体积。
(本小题满分12分)已知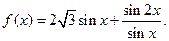
(I)求 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意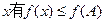 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。