在A、B、C、D四小题中只能选做2题，每小题10，共
计20分。请在答题卡指定区域作答。解答应写出文字
说明、证明过程或演算
步骤。
A、选修4-1：几何证明选讲
如图，已知梯形ABCD为圆内接四边形，AD//BC，过C作该圆的切线，交AD的延长线于E，求证：ΔABC∽ΔEDC。
B、选修4-2：矩形与变换
已知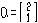
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
C、选修4-4：坐标系与参数方程
在平面直角坐标系xoy中，曲线C的参数方程为
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。
D、选修4-5：不等式选讲
已知a，b都是
正实数，且ab=2。求证：（1+2a）（1+b）≥9。
（本小题10分）已知在三棱锥S--ABC中，∠ACB=900，又SA⊥平面ABC，
AD⊥SC于D，求证：AD⊥平面SBC，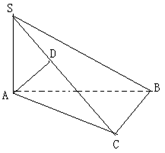
某电器公司生产A型电脑。1993年这种电脑每台平均生产成本为5 000元，并以纯利润20%确定出厂价。从1994年开始，公司通过更新设备和加强管理，使生产成本逐年降低。到1997年，尽管A型电脑出厂价仅是1993年的80%，但却实现了50%纯利润的高效益。
（1）求1997年每台A型电脑的生产成本；
（2）以1993年的生产成本为基数，求1993～1997年生产成本平均每年降低的百分数（精确到0.01，以下数据可供参考：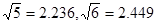
）。
如图，已知底角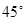
的等腰梯形ABCD，底边BC长为7cm,腰长为
cm，当一条垂直于底边BC（垂足为F）的直线l从左至右移动（与梯形ABCD有公共点）时，直线l把梯形分成两部分，令BF=
，试写出左边部分的面积
与的函数解析式，并画出大致图象。
已知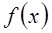
是定义在R上的奇函数，且当
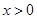时，f(x)=log2x求
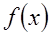的解析式。
已知函数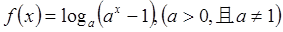
，
（1）求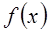
的定义域；（2）讨论函数
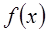的单调性。