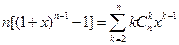、如图,一块半径为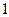 ,圆心角为
,圆心角为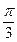 的扇形木板
的扇形木板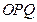 ,现要用其截出一块面积最大的矩形木板,下面提供了两种截出方案,试比较两种方案截出的最大矩形面积哪个最大?请说明理由。
,现要用其截出一块面积最大的矩形木板,下面提供了两种截出方案,试比较两种方案截出的最大矩形面积哪个最大?请说明理由。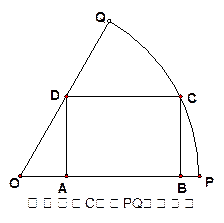
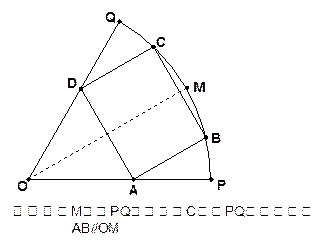
某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰。已知某选手能正确回答第一、二、三、四轮的问题的概率分别为 且各轮问题能否正确回答互不影响。
且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率
已知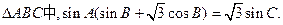
(Ⅰ)求角A的大小 ;
;
(Ⅱ)若BC=3,求 周长的取值范围。
周长的取值范围。
设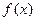 是定义在[-1,1]上的奇函数,且对任意
是定义在[-1,1]上的奇函数,且对任意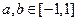 ,当
,当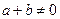 时,都有
时,都有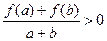 .
.
(1)若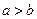 ,试比较
,试比较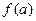 与
与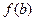 的大小;
的大小;
(2)解不等式
(3)如果 和
和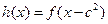 这两个函数的定义域的交集为空集,求
这两个函数的定义域的交集为空集,求 的取值范围.
的取值范围.
在数列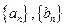 中,
中, 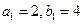 ,且
,且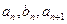 成等差数列,
成等差数列, 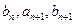 成等比数列
成等比数列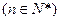 .
.
(1)求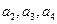 及
及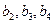 ,由此猜测
,由此猜测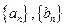 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明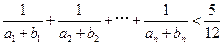 .
.
请先阅读:在等式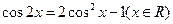 的两边对x求导
的两边对x求导
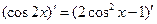 .由求导法则得
.由求导法则得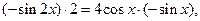 化简后得等式
化简后得等式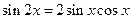 利用上述想法(或者其他方法),试由等式
利用上述想法(或者其他方法),试由等式
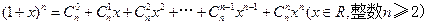 ,
,
证明