某中学七年级有8个班,要从中选出2个班代表学校参加某项活动。七(1)班必须参加,另外再从七(2)至七(8)班选出1个班.七(5)班有学生建议用如下的方法:从装有四个标有数字1、2、3、4的球袋中摸出1个球,记下数字,放回摇匀后再摸出1个球(球的大小、形状与质量完全一样),两次摸出的球上的数字和是几,就选几班。(1)分别求出选七(2)、七(5)、七(8)班的概率;(2)你认为这种方法公平吗?如不公平,请你设计一个公平的方案
某校300名优秀学生,中考数学得分范围是70—119(得分都是整数),为了了解该校这300名学生的中考数学成绩,从中抽查了一部分学生的数学分数,通过数据处理,得到如下频率分布表和频率分布直方图.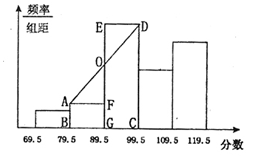
| 分组 |
频数 |
频率 |
| 109.5—119.5 |
15 |
0.30 |
| 99.5--109.5 |
10 |
0.20 |
| 89.5—99.5 |
18 |
|
| 79.5—89.5 |
||
| 69.5—79.5 |
3 |
0.06 |
| 合计 |
1.00 |
请你根据给出的图标解答:
(1)填写频率分布表中未完成部分的数据;
(2)指出在这个问题中的总体和样本容量;
(3)求出在频率分布直方图中直角梯形ABCD的面积;
(4)请你用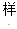
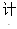
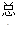
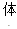 ,可以得到哪些信息?(写一条即可)
,可以得到哪些信息?(写一条即可)
已知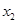
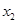 是关于
是关于 的一元二次方程
的一元二次方程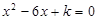 的两个实数根,且
的两个实数根,且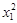
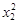 —
— —
—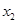 =115
=115
(1)求k的值;(2)求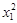 +
+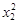 +8的值。
+8的值。
如图,已知:在四边形ABFC中,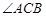 =90
=90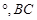 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE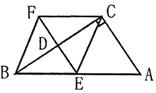
(1)试探究,四边形BECF是什么特殊的四边形;
(2)当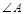 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)
解不等式组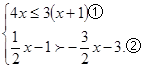 并把解集在已画好的数轴上表示出来。
并把解集在已画好的数轴上表示出来。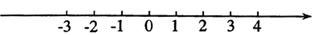
如图,抛物线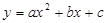 与
与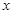 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当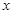 =O和
=O和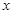 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。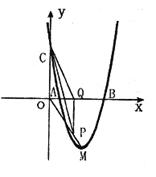
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥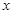 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。