航天飞机，可将物资运送到空间站，也可维修空间站出现的故障。
（1）若已知地球半径为R，地球表面重力加速度为g，某次维修作业中，与空间站对接的航天飞机的速度计显示飞机的速度为v，则该空间站轨道半径R′为多大？
（2）为完成某种空间探测任务，在空间站上发射的探测器通过向后喷气而获得反冲力使其启动。已知探测器的质量为M，每秒钟喷出的气体质量为m，为了简化问题，设喷射时探测器对气体做功的功率恒为P，在不长的时间 内探测器的质量变化较小，可以忽略不计。求喷气t秒后探测器获得的动能是多少？
将一个物体以10m/s的速度从10m的高度水平抛出，落地点与抛出点间的水平距离是多少？（不计空气阻力，去g=10m/s2）
游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来，如图甲所示。我们把这种情况抽象为如图乙所示的模型：半径为R的圆弧轨道竖直放置，下端与弧形轨道相接，使质量为m的小球从弧形轨道上端无初速度滚下，小球进入圆轨道下端后沿圆轨道运动。实验表明，只要h大于一定值，小球就可以顺利通过圆轨道的最高点。（不考虑空气及摩擦阻力）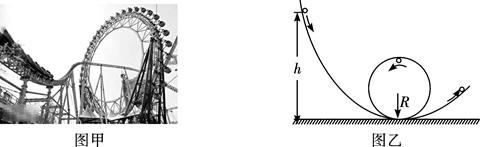
（1）若小球恰能通过最高点，则小球在最高点的速度为多大? 此时对应的h多高？
（2）若h′=4R，则小球在通过圆轨道的最高点时对轨道的压力是多少？
在第21届温哥华冬奥会上，我国女子冰壶队取得了优异的成绩，比赛中，冰壶在水平冰面上的运动可视为匀减速直线运动，设一质量m=20kg的冰壶从被运动员推出到静止共用时t=20s，运动的位移x=30m，取g=10m/s2，求：冰壶在此过程中
（1）平均速度的大小；
（2）加速度的大小；
（3）所受平均阻力的大小。
在真空中A点有一正电荷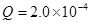
C，把检验电荷
C的负电荷置于B点，他们相距离
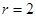m，如图所示。求：
（1）q受到的电场力的大小（k=9.0×109N·m2/c2）；
（2）q所在点的电场强度的大小；
（3）只将B处的检验电荷q移走，求此时B点的电场强度的大小。
如图所示，质量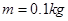
的金属小球从距水平面
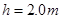的光滑斜面上由静止开始释放，运动到A点时无能量损耗，水平面
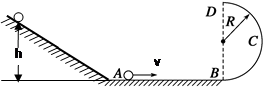
的粗糙平面, 与半径为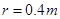
的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内， D为轨道的最高点，小球恰能通过最高点D, 完成以下要求（
）
（1）小球运动到A点时的速度为多大？
（2）小球从A运动到B时摩擦阻力所做的功
（3）小球从B点飞出后落点E与A相距多少米？