2 011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
| 分组 |
频数 |
频率 |
|
| 一组 |
0 <5 <5 |
0 |
0 |
| 二组 |
5 <10 <10 |
10 |
0.10 |
| 三组 |
10 <15 <15 |
10 |
|
| 四组 |
15 <20 <20 |
|
0.50 |
| 五组 |
20 <25 <25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)求购票时间的平均数
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么 决策一下至少要增加几个窗口?
(本题6分)如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。
理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(__________________________)
∴∠2 =∠CGD(等量代换)
∴CE∥BF(_______________________________)
∴∠=∠BFD(__________________________)
又∵∠B =∠C(已知)
∴∠BFD =∠B()
∴AB∥CD(________________________________)
(本题6分)如图:直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,
∠AED=48°,求∠BDF的度数。
如图,平面直角坐标系中,点B的坐标为(1,2),过点B作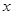 轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与
轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与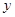 轴交于点F.
轴交于点F.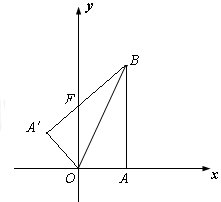
(1)求证:OF=BF;
(2)求BF的长;
(3)求过点A′的双曲线的解析式。
如图,一次函数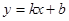 的图像与反比例函数
的图像与反比例函数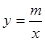 的图像交于
的图像交于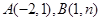 两点。
两点。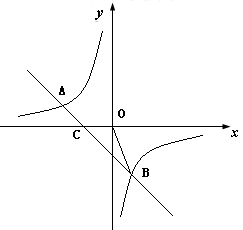
求:(1)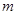 的值;
的值;
(2)求一次函数的解析式;
(3)若直线AB交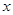 轴于点C,求△OBC的面积.
轴于点C,求△OBC的面积.
.一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.