本小题共13分)
对数列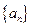 ,规定
,规定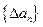 为数列
为数列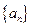 的一阶差分数列,其中
的一阶差分数列,其中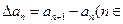 N*).对正整数k,规定
N*).对正整数k,规定 为
为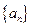 的k阶差分数列,其中
的k阶差分数列,其中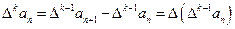 .
.
(Ⅰ)若数列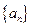 的首项
的首项 ,且满足
,且满足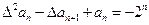 ,求数列
,求数列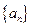 的通项公式;
的通项公式;
(Ⅱ)对(Ⅰ)中的数列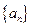 ,若数列
,若数列 是等差数列,使得
是等差数列,使得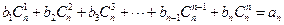 对一切正整数
对一切正整数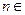 N*都成立,求
N*都成立,求 ;
;
(Ⅲ)在(Ⅱ)的条件下,令 设
设 若
若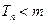 成立,求最小正整数
成立,求最小正整数 的值.
的值.
如图,四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,Q是AD的中点.
,Q是AD的中点.
(Ⅰ)若 ,求证:平面PQB
,求证:平面PQB 平面PAD;
平面PAD;
(Ⅱ)若平面APD 平面ABCD,且
平面ABCD,且 ,点M在线段PC上,试确定点M的位置,使二面角
,点M在线段PC上,试确定点M的位置,使二面角 的大小为
的大小为 ,并求出
,并求出 的值.
的值.
在 中,角
中,角 对的边分别为
对的边分别为 ,已知
,已知 .
.
(Ⅰ)若 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若 ,求
,求 面积的最大值.
面积的最大值.
已知抛物线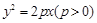 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,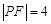 .
.
(1)求抛物线的方程;
(2)设点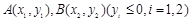 是抛物线上的两点,
是抛物线上的两点,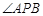 的角平分线与
的角平分线与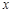 轴垂直,求
轴垂直,求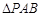 的面积最大时直线
的面积最大时直线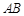 的方程.
的方程.
已知函数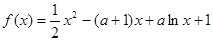
(1)若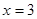 是
是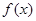 的极值点,求
的极值点,求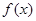 的极大值;
的极大值;
(2)求实数 的范围,使得
的范围,使得 恒成立.
恒成立.
已知正项数列 满足:
满足: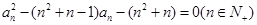 ,数列
,数列 的前
的前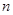 项和为
项和为 ,且满足
,且满足 ,
,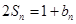
 .
.
(1) 求数列 和
和 的通项公式;
的通项公式;
(2)设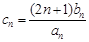 ,数列
,数列 的前
的前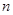 项和为
项和为 ,求证:
,求证: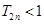 .
.