(本小题共13分)
某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
(Ⅰ)求分别获得一、二、三等奖的概率;
(Ⅱ)设摸球次数为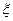 ,求
,求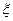 的分布列和数学期望.
的分布列和数学期望.
已知: 为常数)
为常数)
(1)若 ,求
,求 的最小正周期;
的最小正周期;
(2)若 在[
在[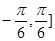 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求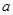 的值.
的值.
如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形,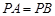 ,且侧面
,且侧面 平面
平面 ,点
,点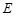 是棱
是棱 的中点.
的中点.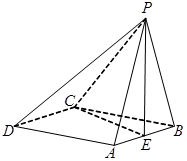
(1)求证: 平面
平面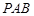 ;
;
(2)求证: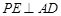 ;
;
(3)若 ,求证:平面
,求证:平面 平面
平面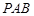 .
.
在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出1个小球,每个小球被取出的可能性相等.
(1)求取出的两个球上的编号都为奇数的概率;
(2)求取出的两个球上的编号之和为3的倍数的概率;
(3)求取出的两个球上的编号之和大于6的概率.
已知等差数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
(1)证明二维形式的柯西不等式:
(2)若实数 满足
满足 求
求 的取值范围.
的取值范围.