(本小题满分14分)如图5,已知 平面
平面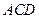 ,
,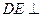 平面
平面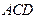 ,△
,△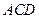 为等边三角形,
为等边三角形,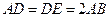 ,
,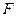 为
为 的中点.
的中点.
(1)求证: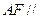 平面
平面 ;(2)求证:平面
;(2)求证:平面 平面
平面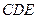 ;
;
(3)求直线 和平面
和平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)
已知椭圆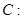
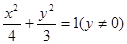 ,其左右焦点分别为
,其左右焦点分别为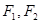 .对于命题
.对于命题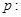 “
“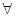 点
点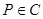 ,
,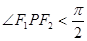 ”.写出
”.写出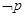 ,判断
,判断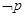 的真假,并说明理由.
的真假,并说明理由.
(本小题满分12分)
(Ⅰ)已知某椭圆的左右焦点分别为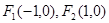 ,且经过点
,且经过点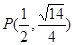 ,求该椭圆的标准方程以及离心率;
,求该椭圆的标准方程以及离心率;
(Ⅱ)某圆锥曲线以坐标轴为对称轴,中心为坐标原点,且过点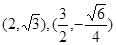 ,求该曲线的标准方程、焦点以及离心率;
,求该曲线的标准方程、焦点以及离心率;
(本小题满分10分)
已知命题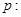 “方程
“方程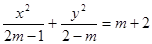 表示的曲线是椭圆”,命题
表示的曲线是椭圆”,命题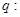 “方程
“方程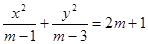 表示的曲线是双曲线”.且
表示的曲线是双曲线”.且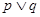 为真命题,
为真命题,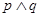 为假命题,求实数
为假命题,求实数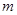 的取值范围.
的取值范围.
(本小题满分14分)如图,已知四边形 是正方形,
是正方形,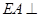 平面
平面 ,
, //
//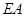 ,
,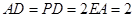 ,
, ,
,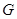 ,
, 分别为
分别为 ,
, ,
, 的中点.
的中点.
(Ⅰ)求证:平面FGH //平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.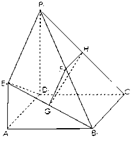
(本小题满分12分)如图,四棱锥S—ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD
(1)求证:SO⊥平面ABCD;
(2)设∠BAD=60°,AB=SD=2,P是侧棱SD上的一点,且SB∥平面APC,求三棱锥A—PCD的体积.