如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域I(r≤R)和圆外区域II(r >R)分别存在两个匀强磁场,方向均垂直于xOy平面。垂直于xOy平面放置两块平面荧光屏,其中荧光屏甲平行于x轴放置在y=—2.2R的位置,荧光屏乙平行于y轴放置在x=3.5R的位置。现有一束质量为m、电荷量为q(q>0)、动能为E0的粒子从坐标为(—R,0)的A点沿x轴正方向射入区域I,最终打在荧光屏甲上,出现亮点N的坐标为(0.4R,—2.2R)。若撤去圆外磁场,粒子也打在荧光屏甲上,出现亮点M的坐标为(0,—2.2R),此时,若将荧光屏甲沿y轴负方向平移,发现亮点的x轴坐标始终保持不变。不计粒子重力影响。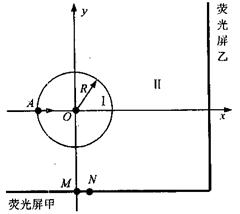
(1)求在区域I和II中粒子运动速度v1、v2的大小;
(2)求在区域I和II中磁感应强度Bl、B2的大小和方向;
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从A点沿x轴正方向射入区域I的粒子束改为质量为m、电荷量为-q、动能为3E0的粒子,求荧光屏上出现亮点的坐标。
如图所示,两个圆形光滑细管在竖直平面内交叠,组成“8”字形通道,在“8”字形通道底端B处连接一内径相同的粗糙水平直管AB。已知E处距地面的高度h=3.2m,一质量m=1kg的小球a从A点以速度v0=12m/s的速度向右进入直管道,到达B点后沿“8”字形轨道向上运动,到达D点时恰好与轨道无作用力,直接进入DE管(DE管光滑),并与原来静止于E处的质量为M=4kg的小球b发生正碰(ab均可视为质点)。已知碰撞后a球沿原路返回,速度大小为碰撞前速度大小的1/3,而b球从E点水平抛出,其水平射程s=0.8m,(g取10m/s2)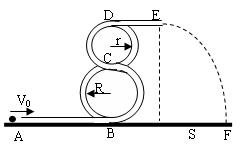
(1)求碰后b球的速度大小?
(2)求“8”字形管道上下两圆的半径r和R.?
(3)若小球a在管道AB中运动时所受阻力为定值,请判断a球返回到BA管道中时能否从A端穿出?
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T
如图所示,P为质量为m=1kg的物块,Q为位于水平地面上的质量为M=4kg的特殊平板,平板与地面间的动摩擦因数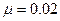 。在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN。P刚从距MN高h=5m处由静止开始自由落下时,板Q向右运动的速度为v0=4m/s。当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用力竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触。在水平方向 上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计。(取g=10m/s2,以下计算结果均保留两位有效数字)求:
。在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN。P刚从距MN高h=5m处由静止开始自由落下时,板Q向右运动的速度为v0=4m/s。当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用力竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触。在水平方向 上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计。(取g=10m/s2,以下计算结果均保留两位有效数字)求:
(1)P第一次落到MN边界的时间t和第一次在相互作用区域中运动的时间T;
(2)P第2次经过MN边界时板Q的速度v;
(3)从P第1次经过MN边界到第2次经过MN边界的过程中,P、Q组成系统损失的机械能△E;
(4)当板Q的速度为零时,P一共回到出发点几次?
1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。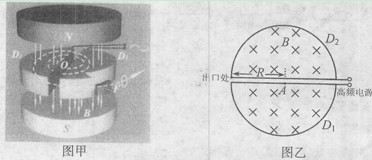
某型号的回旋加速器的工作原理如图甲所示,图乙为俯视图。回旋加速器的核心部分为D形盒,D形盒装在真空容器里,整个装置放在巨大的电磁铁两极之间的强大磁场中,磁场可以认为是匀强磁场,且与D形盒底面垂直。两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计,D形盒的半径力R,磁场的磁感应强度为B。设质子从粒子源A处进入加速电场的初速度不计。质子质量为m、电荷量为+q。加速器接一定频率高频交变电源,其电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求质子第1次经过狭缝被加速后进人D形盒运动的轨道半径r1;
(2)求质子从静止开始加速到出口处所需的时间t;
(3)如果使用这台回旋加速器加速α粒子,需要进行怎样的改动?请写出必要的分析与推理。
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L=1m,导轨平面与水平面成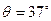 ,下端连接阻值为R的电阻。匀强磁场方向垂直导轨平面向上,磁感应强度B =0.4T。质量m=0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直且保持良好接触,它们间的动摩擦因数μ=0.25。金属棒沿导轨由静止开始下滑,当金属棒下滑速度达到稳定时,速度大小为10 m/s(取g=10m/s2,sin 37°=0.6,cos37°=0.8)。求:
,下端连接阻值为R的电阻。匀强磁场方向垂直导轨平面向上,磁感应强度B =0.4T。质量m=0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直且保持良好接触,它们间的动摩擦因数μ=0.25。金属棒沿导轨由静止开始下滑,当金属棒下滑速度达到稳定时,速度大小为10 m/s(取g=10m/s2,sin 37°=0.6,cos37°=0.8)。求:
(1)金属棒沿导轨开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时电阻R消耗的功率;
(3)电阻R的阻值。