在函数 中,自变量x的取值范围是()
中,自变量x的取值范围是()
A. |
B. |
C. |
D. |
两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的()
| A.众数 | B.方差 | C.中位数 | D.以上都不对 |
一元二次方程2x2-7x+k=0的一个根是x1=2,则另一个根和k的值是()
| A.x2=1,k=4 | B.x2=-1,k=-4 |
C.x2= ,k=6 ,k=6 |
D.x2= ,k=-6 ,k=-6 |
计算 的值是()
的值是()
A. |
B.3 | C.2 | D.2 |
有一段 “三段论”推理是这样的:对于可导函数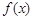 ,若
,若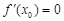 ,则
,则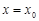 是函数
是函数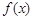 的极值点.因为
的极值点.因为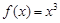 在
在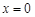 处的导数值
处的导数值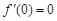 ,所以
,所以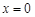 是
是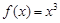 的极值点.以上推理中 ()
的极值点.以上推理中 ()
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |