某港口
 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口 北偏西
北偏西 且与该港口相距
且与该港口相距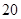 海里的
海里的 处,并正以
处,并正以 海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过 小时与轮船相遇。
小时与轮船相遇。
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(3)是否存在 ,使得小艇以
,使得小艇以 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定
海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
(本小题满分13分)(第一问8分,第二问5分)
已知函数f(x)=2lnx,g(x)= ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[f′(x)-g′(x)]=-3x2-(a+6)x+1.其中f′(x),g′(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由.
广东某品牌玩具企业的产品以往专销欧州市场,在欧债危机的影响下,欧州市场的销量受到严重影响,该企业在政府的大力扶助下积极开拓国内市场,主动投入内销产品的研制开发,并基本形成了市场规模,自2010年9月以来的第n个月(2010年9月为每一个月),产品的内销量、出口量和销售总量(内销量与出口量的和)分别为bn、cn和an(单位万件),分析销售统计数据发现形成如下营销趋势:bn+1=aan,cn+1=an+ba (其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(1)求a,b的值,并写出an+1与an满足的关系式;
(2)如果该企业产品的销售总量an呈现递增趋势,且控制在2万件以内,企业的运作正常且不会出现资金危机;试证明:an<an+1<2.
(3)试求从2010年9月份以来的第n个月的销售总量an关于n的表达式.
(本小题满分12分)
定义在非零实数集上的函数 满足关系式
满足关系式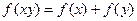 且
且 在区间
在区间 上是增函数
上是增函数
(1)判断函数 的奇偶性并证明你的结论;
的奇偶性并证明你的结论;
(2)解不等式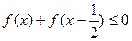
(本小题满分12分)
已知锐角△ABC的三内角A、B、C的对边分别是a、b、c,且(b2+c2-a2)tanA=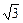 bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1-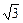 tan(A-10°)]的值.
tan(A-10°)]的值.
(本小题满分12分)
已知向量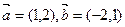 ,
,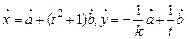 ,k,t为实数.
,k,t为实数.
(Ⅰ)当k=-2时,求使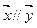 成立的实数t值;
成立的实数t值;
(Ⅱ)若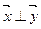 ,求k的取值范围.
,求k的取值范围.