设平面向量
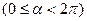 ,
,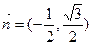
(1)证明;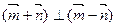
(2)当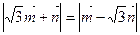 ,求
,求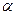 .
.
在△ABC中,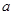 、
、 、
、 分别是角
分别是角 、
、 、
、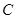 的对边,且
的对边,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若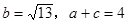 ,求△ABC的面积.
,求△ABC的面积.
函数 是定义在(-1,1)上的单调递增的奇函数,且
是定义在(-1,1)上的单调递增的奇函数,且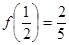
(Ⅰ)求函数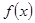 的解析式;
的解析式;
(Ⅱ)求满足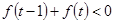 的
的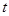 的范围;
的范围;
已知函数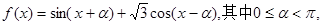 且对于任意实数
且对于任意实数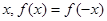 恒成立。
恒成立。
(1)求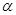 的值;
的值;
(2)求函数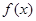 的最大值和单调递增区间。
的最大值和单调递增区间。
已知集合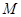 ={
={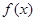 |在定义域内存在实数
|在定义域内存在实数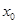 ,使得
,使得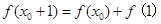 成立}
成立}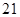
(Ⅰ)函数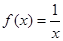 是否属于集合
是否属于集合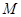 ?说明理由;
?说明理由;
(Ⅱ)证明:函数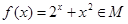 ;.
;.
(Ⅲ)设函数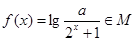 ,求实数a的取值范围.
,求实数a的取值范围.
某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量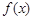 与产量
与产量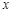 件之间的关系式为:
件之间的关系式为: 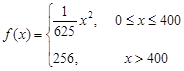 ,每件产品的售价
,每件产品的售价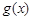 与产量
与产量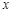 之间的关系式为:
之间的关系式为: 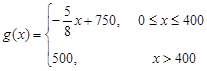 .
.
(Ⅰ)写出该陶瓷厂的日销售利润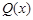 与产量
与产量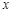 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.