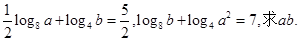已知函数y= (a2x)·
(a2x)·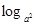 (
(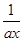 )(2≤x≤4)的最大值为0,最小值为-
)(2≤x≤4)的最大值为0,最小值为-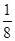 ,求a的值.
,求a的值.
已知函数f(x)=3x+k(k为常数),A(-2k,2)是函数y= f-1(x)图象上的点.
(1)求实数k的值及函数f-1(x)的解析式;
(2)将y= f-1(x)的图象按向量a=(3,0)平移,得到函数y=g(x)的图象,若2 f-1(x+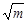 -3)-g(x)≥1恒成立,试求实数m的取值范围.
-3)-g(x)≥1恒成立,试求实数m的取值范围.
若f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1).
(1)求f(log2x)的最小值及对应的x值;
(2)x取何值时,f(log2x)>f(1)且log2[f(x)]<f(1)?
甲、乙两人解关于 的方程:
的方程: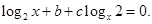 甲写错了常数b,得到根为
甲写错了常数b,得到根为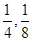 ,乙写错了常数c,得到根为
,乙写错了常数c,得到根为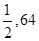 .求方程的真正根。
.求方程的真正根。
已知