ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC= CF=2a,DE=a, P为AB的中点.
(1)求证:平面PCF⊥平面PDE;
(2)求证:AE∥平面BCF.
已知函数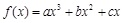 (
(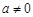 )是定义在
)是定义在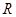 上的奇函数,且
上的奇函数,且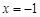 时,函数
时,函数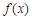 取极值1.
取极值1.
(Ⅰ)求函数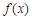 的解析式;
的解析式;
(Ⅱ)令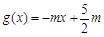 ,若
,若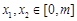 (
(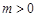 ),不等式
),不等式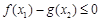 恒成立,求实数
恒成立,求实数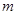 的取值范围;
的取值范围;
已知数列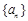 的前n项和为
的前n项和为 ,
,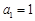 ,且
,且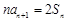 ,数列
,数列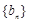 满足
满足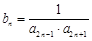 ,数列
,数列 的前n项和为
的前n项和为 (其中
(其中 ).
).
(Ⅰ)求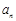 和
和 ;
;
(Ⅱ)若对任意的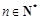 ,不等式
,不等式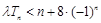 恒成立,求实数
恒成立,求实数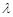 的取值范围
的取值范围
在正三角形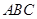 中,
中,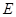 、
、 、
、 分别是
分别是 、
、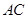 、
、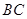 边上的点,满足
边上的点,满足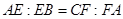
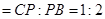 (如图1).将△
(如图1).将△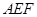 沿
沿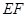 折起到
折起到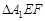 的位置,使二面角
的位置,使二面角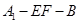 成直二面角,连结
成直二面角,连结 、
、 (如图2)
(如图2)
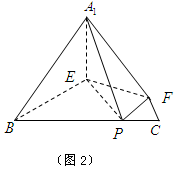
(Ⅰ)求证: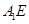 ⊥平面
⊥平面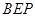 ;
;
(Ⅱ)求二面角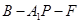 的余弦值.
的余弦值.
某市为了推动全民健身运动在全市的广泛开展,该市电视台开办了健身竞技类栏目《健身大闯关》,规定参赛者单人闯关,参赛者之间相互没有影响,通过关卡者即可获奖。现有甲、乙、丙 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为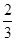 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。
(Ⅰ)求三人中恰有一人获奖的概率;
(Ⅱ)求三人中至少有两人获奖的概率。
已知函数 ,记
,记 的内角
的内角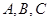 的对边长分别为
的对边长分别为 ,若
,若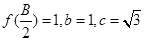 ,求
,求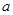 的值。
的值。