在轻质弹簧下端悬挂一质量为0.1kg的物体,当物体静止后,弹簧伸长了0.01m,取g=10m/s2。该弹簧的劲度系数为
| A.1N/m | B.10N/m | C.100N/m | D.1000N/m |
如图所示,三辆相同的平板小车a、b、c成一直线排列,静止在光滑水平地面上,c车上一个小孩跳到b车上,接着又立即从b车跳到a车上,小孩跳离c车和b车时对地的水平速度相同,他跳到a车上没有走动便相对a车保持静止,此后
| A.a、c两车的运动速率相等 |
| B.a、b两车的运动速率相等 |
| C.三辆车的运动速率关系为vc>va>vb |
| D.a、c两车的运动方向一定相同 |
把一支枪水平固定在小车上,小车放在光滑的水平面上,枪发射出一颗子弹时,关于枪、弹、车,下列说法正确的是
| A.枪和子弹组成的系统,动量守恒 |
| B.枪和车组成的系统,动量守恒 |
| C.若忽略不计子弹和枪筒之间的摩擦,枪、车和子弹组成系统的动量才近似守恒 |
| D.枪、车和子弹组成系统的动量守恒 |
关于晶体和非晶体,下列说法正确的是
| A.金刚石、食盐、玻璃和水晶都是晶体 |
| B.晶体的分子(或原子、离子)排列是有规则的 |
| C.单晶体和多晶体有固定的熔点,非晶体没有固定的熔点 |
| D.单晶体和多晶体的物理性质是各向异性的,非晶体是各向同性的 |
如图,水平放置的密封气缸内的气体被一竖直隔板分隔为左右两部分,隔板可在气缸内无摩擦滑动,右侧气体内有一电热丝。气缸壁和隔板均绝热。初始时隔板静止,左右两边气体温度相等。现给电热丝提供一微弱电流,通电一段时间后切断电源。当缸内气体再次达到平衡时,与初始状态相比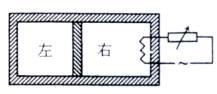
| A.右边气体温度升高,左边气体温度不变 |
| B.左右两边气体温度都升高 |
| C.左边气体压强增大 |
| D.右边气体内能的增加量等于电热丝放出的热量 |
关于热现象和热学规律,有以下说法中正确的是
| A.布朗运动就是液体分子的运动 |
| B.物体的温度越高,分子平均动能越大 |
| C.分子间的距离增大,分子间的引力增大,分子间的斥力减小 |
| D.第二类永动机不可能制成的原因是违反了能量守恒定律 |