如图所示,一根长L=1.5 m的光滑绝缘细直杆MN,竖直固定在场强为E=1.0×105 N/C、与水平方向成θ=30°角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×1 0一6 C,质量m=1.0×10一2 kg。现将小球B从杆的上端N静止释放,小球B开始运动。(静电力常量k=
0一6 C,质量m=1.0×10一2 kg。现将小球B从杆的上端N静止释放,小球B开始运动。(静电力常量k= 9.0×109 N·m2/C2,取g=l0 m/s2)
9.0×109 N·m2/C2,取g=l0 m/s2)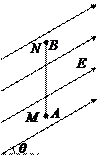
(1)小球B开始运动时的加速度为多大?
(2)小球B的速度最大时,距M端的高度h1为多大?
(3)小球B从N端运动到距M端的高度h2=0.6l m时,速度为v=1.0 m/s,求此过程中小球B的电势能改变了多少?
如图所示的装置,左半部为速度选择器,其有一对平行金属板,两板相距为d,电压为U ;两板之间有匀强磁场,磁感应强度大小为B0,方向与金属板面平行并垂直于纸面朝里,图中右边有一半径为R、圆心为O的圆形区域,区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间,然后沿直线射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区域边界上的G点射出,已知弧
;两板之间有匀强磁场,磁感应强度大小为B0,方向与金属板面平行并垂直于纸面朝里,图中右边有一半径为R、圆心为O的圆形区域,区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间,然后沿直线射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区域边界上的G点射出,已知弧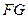 所对应的圆心角为
所对应的圆心角为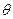 。不计重力,求:
。不计重力,求:
(1)离子速 度
度 的大小;
的大小;
(2)离子的质量。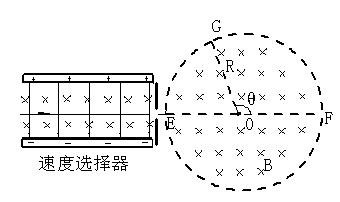
如图所示,有一电子(质量为m,电荷量的绝对值为e),由静止经电压为Uo的加速电场加速后,沿两块水平正对且平行放置的金属板的中线进入板间。已知两块金属板间的距离为d、板间的电压为U,若电子刚好擦着板的边缘射出电场。不计重力,求:
(1)电子射出加速电场时的速率
(2)金属板的长度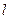
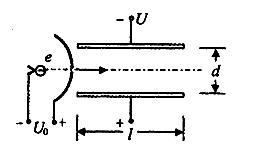
如图所示,一束带负电的离子(电荷量的绝对值为e),以速度v垂直射入磁感强度为B,宽度为d的匀强磁场中,穿透磁场时速度方向与原来入射方向的夹角是60°,不计重力,求:
(1)离子的质量
(2)离子穿过磁场的时间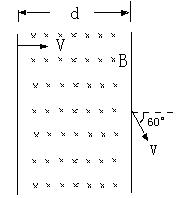
右图是一组匀强电场的电场线,把电量为q =-1.0×10-6C的负电荷从A点移动到B点,知电场强度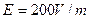 ,A、B间距离d=2m,求:
,A、B间距离d=2m,求:
(1)A、B两点间的电势差多大?
(2)把电荷从A点移动到B点时电场力所做的功?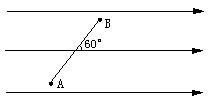
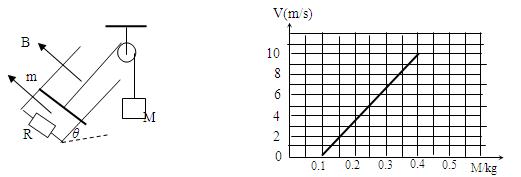
如 图所示,两根与水平面成θ=30°角的足够长光滑金属导轨平行放置,导轨间距为L=1m,导轨底端接有阻值为1 W的电阻R,导轨的电阻忽略不计。整个装置处于匀强磁场中,磁场方向垂直于导轨平面斜向上,磁感应强度B=1T。现有一质量为m=0.2 kg、电阻不计的金属棒用细绳通过光滑滑轮与质量为M=0.5 kg的物体相连,细绳与导轨平面平行。将金属棒与M由静止释放,棒沿导轨运动了2 m后开始做匀速运动。运动过程中,棒与导轨始终保持垂直接触。(取重力加速度g=10m/s2)求:
图所示,两根与水平面成θ=30°角的足够长光滑金属导轨平行放置,导轨间距为L=1m,导轨底端接有阻值为1 W的电阻R,导轨的电阻忽略不计。整个装置处于匀强磁场中,磁场方向垂直于导轨平面斜向上,磁感应强度B=1T。现有一质量为m=0.2 kg、电阻不计的金属棒用细绳通过光滑滑轮与质量为M=0.5 kg的物体相连,细绳与导轨平面平行。将金属棒与M由静止释放,棒沿导轨运动了2 m后开始做匀速运动。运动过程中,棒与导轨始终保持垂直接触。(取重力加速度g=10m/s2)求:
(1)金属棒匀速运动时的速度;
(2)棒从释放到开始匀速运动的过程中,电阻R上产生的焦耳热;
(3)若保持某一大小的磁感应强度B1不变,取不同质量M的物块拉动金属棒,测出金属棒相应的做匀速运动的v值,得到实验图像如图所示,请根据图中的数据计算出此时的B1;