设函数 在
在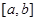 上均可导,且
上均可导,且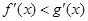 ,则当
,则当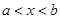 时,有( )
时,有( )
A.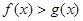 |
B.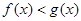 |
C.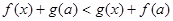 |
D.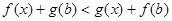 |
用数学归纳法证明不等式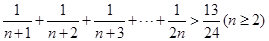 的过程中,
的过程中,
由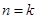 递推到
递推到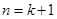 时的不等式左边()
时的不等式左边()
A.增加了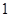 项 项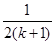 |
B.增加了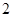 项 项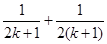 |
C.增加了“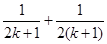 ”,又减少了“ ”,又减少了“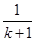 ” ” |
D.增加了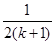 ,减少了“ ,减少了“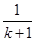 ” ” |
设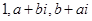 是一等比数列的连续三项,则a,b的值为()
是一等比数列的连续三项,则a,b的值为()
A. |
B.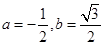 |
C.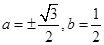 |
D.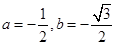 |
给出以下命题:(1)若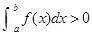 ,则
,则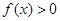 ; (2)
; (2)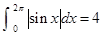 ;
;
(3)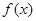 的原函数为
的原函数为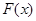 ,且
,且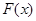 是以
是以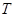 为周期的函数,则
为周期的函数,则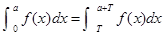 ;
;
其中正确命题的个数为()
A.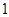 |
B.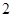 |
C.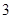 |
D. |
下列几种推理中是演绎推理的序号为()
A.由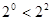 , ,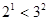 , ,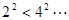 猜想 猜想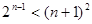 ( (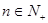 ) ) |
B.半径为r的圆的面积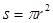 ,单位圆的面积 ,单位圆的面积 |
C.猜想数列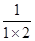 、 、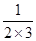 、 、 的通项为 的通项为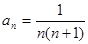 ( (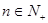 ) ) |
D.由平面直角坐标系中,圆的方程为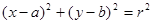 推测空间直角坐标系中球的方程为 推测空间直角坐标系中球的方程为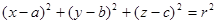 |