如图,在平面直角坐标系中,四边形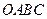 为矩形,
为矩形,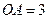 ,
,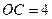 ,
,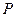 为直线
为直线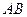 上一动点,将直线
上一动点,将直线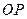 绕点
绕点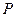 逆时针方向旋转
逆时针方向旋转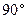 交直线
交直线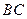 于点
于点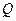 ;
;
(1)当点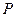 在线段
在线段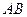 上运动(不与
上运动(不与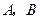 重合)时,求证:OA·BQ=AP·BP;
重合)时,求证:OA·BQ=AP·BP;
(2)在(1)成立的条件下,设点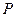 的横坐标为
的横坐标为 ,线段
,线段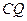 的长度为
的长度为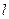 ,求出
,求出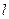 关于
关于 的函数解析式,并判断
的函数解析式,并判断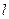 是否存在最小值,若存在,请求出最小值;若不存在,请说明理由。
是否存在最小值,若存在,请求出最小值;若不存在,请说明理由。
(3)直线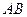 上是否存在点
上是否存在点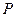 ,使
,使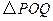 为等腰三角形,若存在,请求出点
为等腰三角形,若存在,请求出点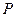 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数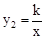 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.
如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD.
(1)求证:CD是⊙O的切线;(2)若AC=2,BC=3,求AB的长.
小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.
如图,海中有一小岛B,它的周围15海里内有暗礁.有一货轮以30海里/时的速度向正北航行半小时后到达C处,发现B岛在它的东北方向.问货轮继续向北航行有无触礁的危险?(参考数据: )
)
某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.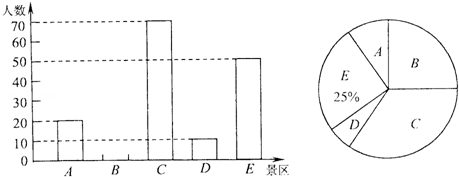
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.