如图所示、传送带的水平部分AB长为=5米,以V0=4m/s的速度向右匀速运动,水平台面与传送带平滑连接与B点,BC长S=1米,台面右边有高为h=0.5m的光滑曲面CD。一质量m=1kg的工件(可以视为质点),从A点无初速度释放,工件与传送带及台面间的动摩擦因数均为0.2,g=10米每二次方秒,求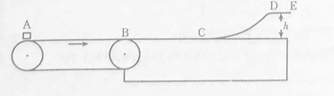
(1)工件运动到B点时的速度大小
(2)通过计算说明,工件能否通过D点到达上平台DE上。
奥巴马同学利用数码相机连拍功能(此相机每秒连拍10张),记录下北京奥运会跳水比赛中小将陈若琳和王鑫在10 m跳台跳水的全过程.所拍摄的第一张恰为她们起跳的瞬间,第四张如图甲所示,王兵同学认为这是她们在最高点;第十九张如图乙所示,她们正好身体竖直双手触及水面.设起跳时她们的重心离台面的距离和触水时她们的重心离水面的距离相等.由以上材料(g取10 m/s2)
(1)估算陈若琳的起跳速度;
(2)通过计算分析第四张照片是在最高点吗?如果不是,此时重心是处于上升还是下降阶段?
高速公路给人们带来极大方便,但由于在高速公路上行驶的汽车速度很大,雾天曾出现过几十辆车追尾相撞的事故,造成极大的人生伤害和财产损失。现假设某条高速公路限制速度为120km/h,某种雾天的能见度(即观察者与能看见的最远目标间的距离)为37m,汽车紧急制动的最大加速度大小为8m/s2,制动时司机的反应时间(即司机发现状况到踩下刹车的时间,该时间内汽车仍然匀速运动)为0.6s,求:
⑴当汽车速度为120km/h时,突然以8m/s2的最大加速度紧急制动,从踩下刹车到汽车停止运动,汽车滑行的距离x;
⑵在该雾天,为了安全,汽车行驶的最大速度v。
如图所示,在光滑水平面上,木块A的质量 ,木块B的质量
,木块B的质量 ,质量
,质量 的木块C置于足够长的木块B上,B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止,A以
的木块C置于足够长的木块B上,B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止,A以 的初速度向右运动,与B碰撞后B的速度为3.5 m/s,碰撞时间极短。求:
的初速度向右运动,与B碰撞后B的速度为3.5 m/s,碰撞时间极短。求:
①A、B碰撞后A的速度。
②弹簧第一次恢复原长时C的速度。
质量为60kg的人,不慎从20m的空中支架上跌落,由于弹性安全带的保护,使他悬在空中,己知安全带长为5m,其缓冲时间是1.2s,则安全带受到的平均冲力大小是多少?(不考虑空气阻力,g=10m/s2)
如图,长为L=2m、质量mA=4kg的木板A放在光滑水平面上,质量mB=1kg的小物块(可视为质点)位于A的中点,水平力F作用于A.AB间的动摩擦因素μ=0.2(AB间最大静摩擦力等于滑动摩擦力,g=10m/s2)。求:
(1)为使AB保持相对静止,F不能超过多大?
(2)若拉力F=12N,物块B从A板左端滑落时木板A的速度为多大?